Bdtyktl

Em matemática, uma função composta é criada aplicando uma função à saída, ou resultado, de uma outra função, sucessivamente. Como uma função deve possuir um domínio e contradomínio bem definidos e estamos falando de aplicar funções mais de uma vez, devemos ser precisos com relação a como estamos aplicando estas funções.

Definição |

Seja:

f:A→B{displaystyle f:Arightarrow B}

e

g:C→D;B⊂C{displaystyle g:Crightarrow D;quad Bsubset C}

duas funções, Se o domínio de g contiver a imagem de f, podemos definir a função composta:

g∘f:A→D{displaystyle gcirc f:Arightarrow D}

como:

g∘f(x)=g(f(x));∀x∈A{displaystyle gcirc f(x)=g(f(x));quad forall xin A}

Isto é ilustrado na figura abaixo:

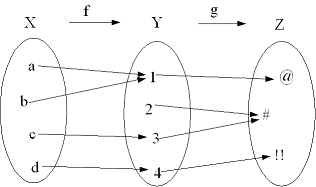
Associatividade |

Pode-se então estender a definição para a composição de três ou mais funções, de maneira análoga. Sejam

f:A→B, g:B→C e h:C→D{displaystyle f:Arightarrow B{mbox{, }}g:Brightarrow C{mbox{ e }}h:Crightarrow D}.

É fácil mostrar que:

(h∘g)∘f=h∘(g∘f){displaystyle (hcirc g)circ f=hcirc (gcirc f),}

Por transitividade e associatividade, define-se a função composta:

h∘g∘f:A→D{displaystyle hcirc gcirc f:Arightarrow D}

como:

(h∘g∘f)(x)=(h∘g)(f(x))=h(g(f(x)))∀ x∈A{displaystyle (hcirc gcirc f)(x)=(hcirc g)(f(x))=h(g(f(x)))quad forall xin A}

De uma forma geral, basta a imagem f(A){displaystyle f(A)} estar contida no domínio de g para podermos definir a função composta g∘f{displaystyle gcirc f} (a definição rigorosa seria uma composição com a função inclusão).

Potência de uma função |

Seja f:A→A{displaystyle f:Arightarrow A,}. Neste caso, pode-se definir f∘f{displaystyle fcirc f,}, f∘f∘f{displaystyle fcirc fcirc f,}, etc. Pode-se portanto definir fn{displaystyle f^{n},} (por indução: fn∘f=f∘fn=fn+1{displaystyle f^{n}circ f=fcirc f^{n}=f^{n+1},}) para n≥2{displaystyle ngeq 2,}. Definindo-se:

f0=IdA{displaystyle f^{0}={mbox{Id}}_{A},}

f1=f{displaystyle f^{1}=f,}

Chega-se facilmente a:

fn∘fm=fn+m{displaystyle f^{n}circ f^{m}=f^{n+m},}

Eventualmente, conforme a estrutura do conjunto A e da função f, é possível estender a definição de fn{displaystyle f^{n},} para n inteiro (ou mesmo outros superconjuntos dos naturais).

Ver também |

Outros projetos Wikimedia também contêm material sobre este tema:
	Livros e manuais no Wikilivros