Bdtyktl

A função inversa g{displaystyle g} de uma função real de variável real f{displaystyle f} obtém-se de f{displaystyle f} por uma simetria em relação à recta y=x{displaystyle y=x}.

Em matemática, a função inversa de uma função f:X→Y{displaystyle f:Xrightarrow Y} é, quando existe, a função f−1:Y→X{displaystyle f^{-1}:Yrightarrow X} tal que f∘f−1=idY{displaystyle fcirc f^{-1}=mathrm {id} _{Y}} e f−1∘f=idX{displaystyle f^{-1}circ f=mathrm {id} _{X}} (id=função identidade). Ou seja, o que era domínio na função original (o conjunto X{displaystyle X} neste caso, ilustrado na figura abaixo) vira imagem na função inversa, e o que era imagem na função original (Y{displaystyle Y}, neste caso - ilustrado na figura abaixo) vira domínio.

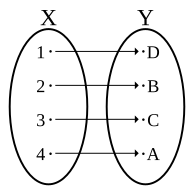
Uma função que tenha inversa diz-se invertível. Se uma função for invertível, então tem uma única inversa. Uma condição necessária e suficiente para que uma função seja invertível é que seja bijectiva^[1].

Se f:X→Y{displaystyle f:Xto Y} for uma função injectiva de X{displaystyle X} em Y{displaystyle Y}, então f{displaystyle f} é também uma função bijectiva de X{displaystyle X} em f(X){displaystyle f(X)}. Consequentemente, tem uma inversa de f(X){displaystyle f(X)} em X{displaystyle X}. Por abuso de linguagem, também se designa esta função por inversa de f{displaystyle f}, embora o seu domínio não seja, em geral, o conjunto Y{displaystyle Y}.

A função inversa de uma função real de uma variável real |

Seja f:R→R{displaystyle f:mathbb {R} to mathbb {R} } uma função bijetiva definida por y=f(x){displaystyle y=f(x)}. Resolvendo y=f(x){displaystyle y=f(x)} para x{displaystyle x} em função de y{displaystyle y}, temos determinado uma função x=g(y){displaystyle x=g(y)}. Esta função é a função inversa de f{displaystyle f}, i.e. g=f−1{displaystyle g=f^{-1}}.^[2]

Exemplo:

Para determinarmos a inversa da função f(x)=x+1{displaystyle f(x)=x+1} podemos proceder da seguinte forma:

1. f(x)=x+1{displaystyle f(x)=x+1}


2. y=x+1{displaystyle y=x+1}


3. x=y+1{displaystyle x=y+1}


4. y=x−1{displaystyle y=x-1}


5. Portanto, f−1(x)=x−1{displaystyle f^{-1}(x)=x-1}
   

Inversa à direita ou à esquerda |

Dadas as funções f:A→B{displaystyle f:Ato B} e g:B→A{displaystyle g:Bto A}, diremos que g{displaystyle g} é função inversa à esquerda de f{displaystyle f}quando a função composta g∘f=idA:A→A{displaystyle gcirc f=id_{A}:Ato A} (id=função identidade), ou seja, quando g(f(x))=x{displaystyle g(f(x))=x} para todo x{displaystyle x} pertencente ao conjunto A. Uma função f{displaystyle f} possui inversa à esquerda se, e somente se, for injectiva.^[3] . Por exemplo, a função f:N→R{displaystyle f:mathbb {N} to mathbb {R} } dada por f(x)=2x{displaystyle f(x)=2x}, que é injetiva e não sobrejetiva, tem como inversa g(x)=x2{displaystyle g(x)={frac {x}{2}}}, porque a função composta (g∘f)(x)=g(f(x))=2x2=x{displaystyle (gcirc f)(x)=g(f(x))={frac {2x}{2}}=x} para todo x∈N{displaystyle xin mathbb {N} }, a qual é a função identidade.

Dadas as funções g:B→A e f:A→B e , diremos que g é uma inversa à direita de f quando a função composta f O g = idB:B→B, ou seja, quando f(g(x)) = x para todo y pertencente ao conjunto B. Uma função f possui inversa à direita se, e somente se, for sobrejetiva.^[3]

Referências

Ver também |

Outros projetos Wikimedia também contêm material sobre este tema:
	Livros e manuais no Wikilivros