Bdtyktl

A tradução deste artigo está abaixo da qualidade média aceitável. É possível que tenha sido feita por um tradutor automático ou por alguém que não conhece bem o português ou a língua original do texto. Caso queira colaborar com a Wikipédia, tente encontrar a página original e melhore este verbete conforme o guia de tradução.

Esta página ou secção cita fontes confiáveis e independentes, mas que não cobrem todo o conteúdo, o que compromete a verificabilidade (desde janeiro de 2013). Por favor, insira mais referências no texto. Material sem fontes poderá ser removido. —Encontre fontes: Google (notícias, livros e acadêmico)

Em álgebra abstrata, um homomorfismo é uma aplicação que preserva a estrutura entre duas estruturas algébricas (como por exemplo grupos, anéis ou espaços vetoriais). A palavra homomorfismo vem da língua grega antiga: ὁμός (homos) significando "mesmo" e μορφή (morphe) significando "formato". Isomorfismos, automorfismos e endomorfismos são tipos especiais de homomorfismos.

Definição e ilustração |

Definição |

A definição de homomorfismo depende do tipo de estrutura algébrica a ser observada. Definições particulares de homomorfismo incluem o que segue:

• Um homomorfismo de semigrupos é uma função que preserva uma operação binária associativa.


• Um homomorfismo de monoides é um homomorfismo de semigrupos que leva a identidade do domínio à identidade do contradomínio.


• Um homomorfismo de grupos é um homomorfismo que preserva a estrutura de grupo. Equivalentemente, é um homomorfismo de semigrupos entre grupos.


• Um homomorfismo de anéis é um homomorfismo que preserva a estrutura de anel. Dependendo da definição de anel que estiver em uso, pode ser exigido ou não que a identidade seja preservada.


• Uma transformação linear é um homomorfismo que preserva a estrutura de espaço vetorial, a saber, a estrutura de grupo abeliano e a multiplicação por escalar. Também é preciso especificar o tipo de escalares considerados, por exemplo, toda aplicação R-linear é uma aplicação Z-linear, mas não vice-versa.


• Um homomorfismo de módulos é um homomorfismo que preserva a estrutura de módulo.


• Um homomorfismo de álgebras é um homomorfismo que preserva a estrutura de álgebra.


• Um functor é um homomorfismo entre duas categorias.

O tema comum é que o homomorfismo é uma função entre dois objetos algébricos que respeita a estrutura algébrica.

Por exemplo, um grupo é um objeto algébrico consistente de um conjunto que junto com uma única operação binária, satisfaça certos axiomas. Se (G,∗){displaystyle (G,*)} e (H,∗′){displaystyle (H,*')} são grupos, um homomorfismo de (G,∗){displaystyle (G,*)} até (H,∗′){displaystyle (H,*')} é uma função ƒ: (G,∗){displaystyle (G,*)} → (H,∗′){displaystyle (H,*')} de tal modo que
f(g1∗g2)=f(g1)∗′f(g2){displaystyle f(g_{1}*g_{2})=f(g_{1})*'f(g_{2})}
para qualquer elemento g1,g2∈G{displaystyle g_{1},g_{2}in G}.

Quando uma estrutura algébrica inclui mais do que uma operação, são necessários homomofismos para preservar cada operação. Por exemplo, um anel possui tanto adição quanto multiplicação, e um homomorfismo do anel (R,+,∗,0,1){displaystyle (R,+,*,0,1)} para o anel (R′,+′,∗′,0′,1′){displaystyle (R',+',*',0',1')} é uma função de tal modo que

f(r+s)=f(r)+′f(s)andf(r∗s)=f(r)∗′f(s){displaystyle f(r+s)=f(r)+'f(s)qquad {text{and}}qquad f(r*s)=f(r)*'f(s)}

para qualquer elemento r e s do domínio do anel.

A noção de homomorfismo pode ser dada uma definição formal no contexto de álgebra universal, campo que estuda as ideias comuns a todas as estruturas algébricas. Neste cenário, um homomorfismo ƒ: A → B é uma função entre duas estruturas algébricas do mesmo tipo de tal modo que

f(μA(a1,…,an))=μB(f(a1),…,f(an)){displaystyle f(mu _{A}(a_{1},ldots ,a_{n}))=mu _{B}(f(a_{1}),ldots ,f(a_{n}))}

para cada n-ary operation μ e para todos os elementos a₁,...,a_n ∈ A.

Exemplos básicos |

Os números reais são um anel, tendo tanto adição quanto multiplicação. o conjunto de todos 2 × 2 matrizes também é um anel, sob adição de matrizes e produto de matrizes. Se nós definirmos uma função entre esses anéis como a seguir:

f(r)=(r00r){displaystyle f(r)={begin{pmatrix}r&0\0&rend{pmatrix}}}

onde r é um número real. Então ƒ é um homomorfismo de anéis, desde que ƒ preserve tanto adição:

f(r+s)=(r+s00r+s)=(r00r)+(s00s)=f(r)+f(s){displaystyle f(r+s)={begin{pmatrix}r+s&0\0&r+send{pmatrix}}={begin{pmatrix}r&0\0&rend{pmatrix}}+{begin{pmatrix}s&0\0&send{pmatrix}}=f(r)+f(s)}

quanto a multiplicação:

f(rs)=(rs00rs)=(r00r)(s00s)=f(r)f(s).{displaystyle f(rs)={begin{pmatrix}rs&0\0&rsend{pmatrix}}={begin{pmatrix}r&0\0&rend{pmatrix}}{begin{pmatrix}s&0\0&send{pmatrix}}=f(r),f(s).}

Por outro exemplo, o diferente de zero número complexos forma um grupo sobe a operação de multiplicação, assim como os números reais diferentes de zero. (Zero precisa ser excluído dos dois grupos desde que não tenha uma inverso multiplicativo, na qual é necessário para elementos do grupo.) Defina a função ƒ a partir do complexo dos números diferentes de zero para os números reais diferentes de zero

f(z)=|z|.{displaystyle f(z)=|z|.}

Que é, ƒ(z) é o função modular (ou módulo) do número complexo z. Então ƒ é um homomorfismo de grupos, desde que isso preserve a multiplicação:

f(z1z2)=|z1z2|=|z1||z2|=f(z1)f(z2).{displaystyle f(z_{1}z_{2})=|z_{1}z_{2}|=|z_{1}|,|z_{2}|=f(z_{1}),f(z_{2}).}

Note que ƒ não é possível estender para um homomorfismo de anéis (a partir dos números complexos para os números reais), já que ele não preserva a adição:

|z1+z2|≠|z1|+|z2|.{displaystyle |z_{1}+z_{2}|neq |z_{1}|+|z_{2}|.}

Discussão informal |

Porque álgebra abstrata estuda conjuntos dotados com operações que geram interessantes estruturas ou propriedade no conjunto, funções que preservam as operações são especialmente importantes. Essas funções são conhecidas como homomorfismos.

Por exemplo, considere o conjunto dos números naturais com adição como a operação. A função que preserva adição deveria ter a propriedade: f(a + b) = f(a) + f(b). Por exemplo, f(x) = 3x é um homomorfismo tal, desde que f(a + b) = 3(a + b) = 3a + 3b = f(a) + f(b). Note que esse homomorfismo mapeia os números naturais de volta para si.

Homomorfismos não têm que mapear conjuntos que têm as mesmas operações. Por exemplo, operação que preserva as funções existe entre o conjunto dos números reais com adição e e o conjunto dos números positivos reais com a multiplicação. A função que preserva operação deveria ter essa propriedade: f(a + b) = f(a) * f(b), já que adição é uma operação no primeiro conjunto e multiplicação [e uma operação no segundo. Dada as leis de exponenciação, f(x) = e^x satisfaz essas condições: 2 + 3 = 5 traduz-se em e² * e³ = e⁵.

Se nós estamos considerando operações múltiplas em um conjunto, então todas as operações devem ser preservadas para a função a ser considerada homomorfismo. Apesar de o conjunto poder ser o mesmo, a mesma função poderá ser um homomorfismo, em teoria dos grupos se diz (conjunto com uma única operação) mas não em teoria dos anéis (conjuntos com duas operações relacionadas), já que isso falha na preservação da operação adicional que a teoria dos anéis considera.

Relação à teoria da categoria |

Uma vez que homomorfismos são s, o seguinte tipos específicos de morfismos definido em qualquer categoria são definidos por homorfismos também. No entanto, as definições em teoria das categorias são um tanto técnicas. No importante caso especial de homomorfismo de módulos, e por outras classes de homomorfismos, há descrições mais simples, como segue:

• Um isomorfismo é um homomorfismo bijetivo .


• Um epimorfismo (às vezes chamado de recobrimento) é um homomorfismo sobrejetivo.


• Um monomorfismo (às vezes chamado de imersão ou extensão) é um homomorfismo injetivo.


• Um endomorfismo é um homomorfismo de um objeto para ele mesmo.


• Um automorfismo é um endomorfismo que é também um isomorfismo, por exemplo, um isomorfismo de um objeto para ele mesmo.

Essas descrições pode ser usadas a fim de obter uma série de propriedades interessantes. Por exemplo, uma vez que a função é bijetiva se e somente se ela é tanto injetiva quanto sobrejetiva, um homomorfismo módulo é um isomorfismo se e somente se é tanto um monomorfismo quanto um epimorfismo.

Para endomorfismos e automorfismos, a descrição acima coincide com a teoria de definição categórica; as primeiras três descrições não. Por exemplo, a precisa definição para o homomorfismo f para ser iso não é apenas ser bijetivo, e assim ter uma inversa f⁻¹, mas também esta inversa é um homomorfismo. Isso tem a importante consequência que dois objetos são completamente indistinguíveis na medida que a estrutura em questão é considerada, se existir um isomorfismo entre elas. Dois objetos assim são ditos isomorfos.

Na realidade, na definição algébrica (pelo menos dentro do contexto de álgebra universal) essa condição extra no isomorfismo é automaticamente satisfeita. No entanto, o mesmo não é verdadeiro para epimorfismos; por exemplo, a inclusão de Z como o (unitário) sub-anel de Q não é sobrejetora, mas uma epimorfia homomorfismo de anéis.^[1] Essa inclusão, portanto, também é um exemplo de um homomorfismo anel que é tanto mono quanto epi, mas não iso.

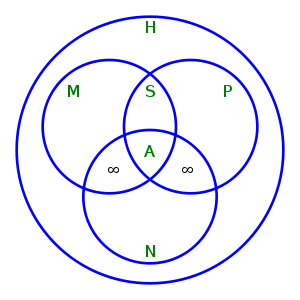
Relações entre diferentes tipos de modulo homomórfico.
H = conjunto de Homomorfismos, M = conjunto de Monomorfismos,
P = conjunto de Epimorfismos, S = conjunto de Isomorfismo,
N = conjunto de Endomorfismo, A = conjunto de Automorfismo.
Perceba que: M ∩ P = S, S ∩ N = A,
(M ∩ N) A and (P ∩ N) A contem somente homomorfismo de modulos infinitos para elas mesmas.

Núcleo de um homomorfismo |

Qualquer homomorfismo f : X → Y define uma relação de equivalência ~ em X por a ~ b se e somente se f(a) = f(b). A relação ~ é chamada de núcleo de f. É uma relação de congruência em X. A classe de equivalência X/~, (conjunto quociente), pode, então, ser dado um objeto estrutura na forma natural, por exemplo [x] * [y] = [x * y]. Nesse caso a imagem de X em Y sob o homomorfismo f é necessariamente isomorfismo para X/~; esse fato é um dos teoremas do isomorfismo. Note que em alguns casos (por exemplo grupos ou anéis), a única classe de equivalência K basta para especificar a estrutura do quociente; então nós podemos escrevê-la X/K. (X/K é usualmente lida como "X mod K".) Também nestes casos, é K, ao invés de ~, que é chamada de núcleo def (cf. subgrupo normal).

Homomorfismos de estruturas relacionais |

Em teoria dos modelos, a noção de uma estrutura algébrica é generalizada para estruturas envolvendo tanto operações quanto relações. Sendo L uma assinatura composta por função e símbolos de relações, e A e B duas L-estruturas. Então o homomorfismo de A para B é um mapeamento h do domínio de A para o domínio de B de tal modo que

• 
  h(F^A(a₁,…,a_n)) = F^B(h(a₁),…,h(a_n)) para cada símbolo de função n-aria F em L,


• 
  R^A(a₁,…,a_n) implica R^B(h(a₁),…,h(a_n)) para cada símbolo de relação n-ary R in L.

Nos casos especiais com somente uma relação binária, nós obtemos a noção de um homomorfismo de grafos.

Homomorfismos e e-livre homomorfismo na teoria da línguagem formal |

Homomorfismos são também usados no estudo de linguagem formal^[2] (embora dentro deste contexto, muitas vezes eles são brevemente referidos aos morfismos^[3]). Dados alfabetos Σ1{displaystyle Sigma _{1}} and Σ2,{displaystyle Sigma _{2},} a função h : Σ1∗{displaystyle Sigma _{1}^{*}} → Σ2∗{displaystyle Sigma _{2}^{*}} de tal modo que h(uv)=h(u)h(v){displaystyle h(uv)=h(u)h(v)} para todo u e v em Σ1∗{displaystyle Sigma _{1}^{*}} é chamado de homomorfismo (ou simplesmente morfismo) em Σ1∗.{displaystyle Sigma _{1}^{*}.} ^[4] Seja e denotando a palavra vazia. Se h é um homomorfismo em Σ1∗{displaystyle Sigma _{1}^{*}} e h(x)≠e{displaystyle h(x)neq e} para todo x≠e{displaystyle xneq e} em Σ1∗,{displaystyle Sigma _{1}^{*},} então h é chamado de homomorfismo e-livre.

Esse tipo de homomorfismo pode ser pensado como (e é equivalente a) um homomorfismo monóide onde Σ∗{displaystyle Sigma ^{*}} o conjunto de todas as palavras ao longo de um alfabeto finito Σ{displaystyle Sigma } é uma monóide (de fato é a monóide livre Σ{displaystyle Sigma }) com operação de concatenação e a palavra vazia como a identificar

Ver também |

• Função contínua


• Difeomorfismo

Referências

Bibliografia |

• Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.