Fórmula de Euler
|
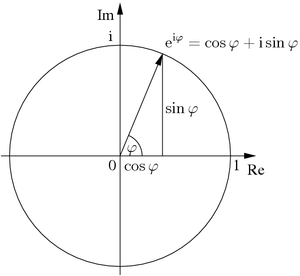
Interpretação geométrica da fórmula de Euler.
A fórmula de Euler, cujo nome é uma homenagem a Leonhard Euler, é uma fórmula matemática da área específica da análise complexa, que mostra uma relação entre as funções trigonométricas e a função exponencial (a identidade de Euler é um caso especial da fórmula de Euler). A fórmula é dada por:[1]
eix=cos(x)+isin(x){displaystyle e^{ix}=cos left(xright)+{text{i}},operatorname {sin} left(xright)},
em que :
x é o argumento real (em radianos);
e é a base do logaritmo natural;
i2=−1{displaystyle {text{i}}^{2}=-1}, onde i{displaystyle {text{i}}}
é a unidade imaginária (número complexo);
sin(x){displaystyle {text{sin}}(x)}e cos(x){displaystyle cos(x)}
são funções trigonométricas.
A relação entre exponencial complexa e funções trigonométricas foi primeiro provada pelo matemático inglês Roger Cotes em 1714, na forma
- ln(cosx+isenx)=ix{displaystyle ln(cos x+{text{i}},{text{sen}}x)={text{i}},x}
em que ln é o logaritmo natural[2]
Índice
1 Prova utilizando cálculo
2 Prova utilizando série de Taylor
3 Exemplo
4 Ver também
5 Referências
6 Ligações externas
Prova utilizando cálculo |
O ponto negro representa um número complexo. Seu valor absoluto é "r", a distãncia da origem. Seu argumento é φ, seu ângulo em radianos
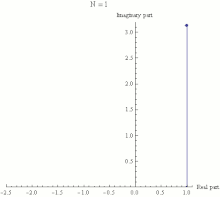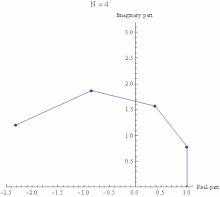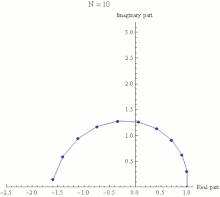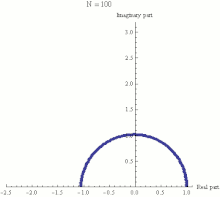
A função exponencial eiπ{displaystyle e^{ipi }}
pode ser definida como o limite de uma sequência (1+iπn)n{displaystyle left(1+{frac {ipi }{n}}right)^{n}}
, quando n tende ao infinito. Nesta animação, "n" assume valores crescentes entre 1 e 100. À medida que n cresce, (1+iπn)n{displaystyle left(1+{frac {ipi }{n}}right)^{n}} se aproxima de -1.
Ver artigo principal: tabela de derivadasVer artigo principal: número complexoVer artigo principal: cossenoVer artigo principal: senoUma propriedade conhecida das funções exponenciais é que elas são iguais às suas derivadas:
ddxex=ex{displaystyle {frac {text{d}}{{text{d}}x}}e^{x}=e^{x}}, onde "x" é um número real.
As funções exponenciais com números complexos também satisfazem esta mesma propriedade[3]:
ddzez=ez{displaystyle {frac {text{d}}{{text{d}}z}}e^{z}=e^{z}}, onde "z" é um número complexo.
Portanto, pela regra da cadeia:
- ddxeix=ieix .{displaystyle {frac {text{d}}{{text{d}}x}}e^{{text{i}}x}={text{i}},e^{{text{i}},x} .}
Então definimos uma nova função, que chamaremos de "f":
- f(x)=(cosx−isinx)⋅eix .{displaystyle f(x)=(cos x-isin x)cdot e^{ix} .}
Pela regra do produto, que vale também para funções que tenham como imagem números complexos, a derivada de f(x) será::
- ddxf(x)=(cosx−isinx)⋅ddxeix+ddx(cosx−isinx)⋅eix=(cosx−isinx)(ieix)+(−sinx−icosx)⋅eix=(icosx+sinx−sinx−icosx)⋅eix=0 .{displaystyle {begin{aligned}{frac {text{d}}{{text{d}}x}}f(x)&=(cos x-{text{i}}sin x)cdot {frac {text{d}}{{text{d}}x}}e^{{text{i}},x}+{frac {text{d}}{{text{d}}x}}(cos x-{text{i}},sin x)cdot e^{{text{i}},x}\&=(cos x-{text{i}},sin x)({text{i}},e^{{text{i}},x})+(-sin x-{text{i}},cos x)cdot e^{{text{i}},x}\&=({text{i}},cos x+sin x-sin x-{text{i}},cos x)cdot e^{{text{i}},x}\&=0 .end{aligned}}}
Portanto, f(x) deve ser uma função constante em x. Já que f(0)=1 (o que pode ser facilmente descoberto substituindo-se x por 0 na função),
- 1=(cosx−isinx)⋅eix .{displaystyle 1=(cos x-{text{i}},sin x)cdot e^{{text{i}},x} .}
Multiplicando os dois lados por cos x + i sin x, obtemos
- cosx+isinx=(cosx+isinx)(cosx−isinx)⋅eix=(cos2x−(isinx)2)⋅eix=(cos2x+sin2x)⋅eix=eix .{displaystyle {begin{aligned}cos x+{text{i}},sin x&=(cos x+{text{i}},sin x)(cos x-{text{i}},sin x)cdot e^{{text{i}},x}\&=(cos ^{2}x-({text{i}},sin x)^{2})cdot e^{{text{i}},x}\&=(cos ^{2}x+sin ^{2}x)cdot e^{{text{i}},x}\&=e^{{text{i}},x} .end{aligned}}}
Prova utilizando série de Taylor |
Para o estudo da fórmula de Euler necessitamos do conhecimento de expansão em séries de potência. Introduziremos uma grande ferramenta, sem uma análise profunda, que é o seguinte conceito:
A expansão em série de Taylor de uma função analítica f(x){displaystyle f(x)}
- f(x)=∑n=o∞Cn(x−a)n{displaystyle f(x)=sum _{n=o}^{infty }{C_{n}}{(x-a)^{n}}}
com |x−a|<R{displaystyle |x-a|<R}
- Cn=fn(a)n!{displaystyle C_{n}={frac {{f^{n}}(a)}{n!}}}
Usando esse conceito de expansão e tomando f(x)=ex{displaystyle f(x)=e^{x}}
- ex=∑n=0∞fn(0)xnn!=∑n=0∞xnn!=1+x1!+x22!+x33!+...+xnn!{displaystyle e^{x}=sum _{n=0}^{infty }{frac {{{f^{n}}(0)}{x^{n}}}{n!}}=sum _{n=0}^{infty }{frac {x^{n}}{n!}}=1+{frac {x}{1!}}+{frac {x^{2}}{2!}}+{frac {x^{3}}{3!}}+{...}+{frac {x^{n}}{n!}}}
para todo x{displaystyle x}
Em x=1{displaystyle x=1}
- e=∑n=0∞1n!=1+11!+12!+13!+...{displaystyle e=sum _{n=0}^{infty }{frac {1}{n!}}=1+{frac {1}{1!}}+{frac {1}{2!}}+{frac {1}{3!}}+{...}}
Se admitirmos a validade de substituirmos x{displaystyle x}
- eix=∑n=0∞(ix)nn!=∑n=0∞(−1)n⋅x2n(2n)!+i∑n=1∞(−1)n−1⋅x2n−1(2n−1)!{displaystyle e^{{text{i}},x}=sum _{n=0}^{infty }{frac {({text{i}},x)^{n}}{n!}}={sum _{n=0}^{infty }{frac {{(-1)^{n}}cdot {x^{2n}}}{(2n)!}}}+{text{i}},{sum _{n=1}^{infty }{frac {{(-1)^{n-1}}cdot {x^{2n-1}}}{(2n-1)!}}}}
A primeira parte da soma da equação anterior (eix{displaystyle e^{ix}}
- eix=cos(x)+isin(x){displaystyle e^{{text{i}},x}=cos left(xright)+{text{i}},,operatorname {sin} left(xright)}
que de forma mais generalizada pode ser escrita como:
eiux=cos(ux)+isin(ux){displaystyle e^{{text{i}},ux}=cos left(uxright)+{text{i}},operatorname {sin} left(uxright)}.
Exemplo |
Se tomarmos como x=π=3,1415....{displaystyle x=pi =3,1415....}
- eiπ=−1{displaystyle e^{{text{i}},pi }=-1}
- eiπ+1=0{displaystyle e^{{text{i}},pi }+1=0}
Ver também |
- Fórmula de De Moivre
Referências
↑ ab SIMON, Carl P., e BLUME, Lawrence. Matemática para Economistas. Porto Alegre: Bookman, 2005. Reimpressão 2008. ISBN 978-85-363-0307-9. Seção A3.4, páginas 871 e 872.
↑ John Stillwell (2002). Mathematics and Its History. Springer.
↑ Daniels, Doug. «Complex Differentiation». Consultado em 15 de maio de 2011
Ligações externas |
- Prova da relação de Euler
