Bdtyktl

Esta página foi marcada para revisão, devido a incoerências e/ou dados de confiabilidade duvidosa (desde fevereiro de 2014). Se tem algum conhecimento sobre o tema, por favor, verifique e melhore a coerência e o rigor deste artigo.

Esta página ou secção cita fontes confiáveis e independentes, mas que não cobrem todo o conteúdo, o que compromete a verificabilidade (desde Agosto de 2011). Por favor, insira mais referências no texto. Material sem fontes poderá ser removido. —Encontre fontes: Google (notícias, livros e acadêmico)

Em matemática, a transformada de Fourier é uma transformada integral que expressa uma função em termos de funções de base sinusoidal. Existem diversas variações diretamente relacionadas desta transformada, dependendo do tipo de função a transformar. A transformada de Fourier, epônimo a Jean-Baptiste Joseph Fourier,^[1] decompõe uma função temporal (um sinal) em frequências, tal como um acorde de um instrumento musical pode ser expresso como a amplitude (ou volume) das suas notas constituintes. A transformada de Fourier de uma função temporal é uma função de valor complexo da frequência, cujo valor absoluto representa a soma das frequências presente na função original e cujo argumento complexo é a fase de deslocamento da base sinusoidal naquela frequência.

A transformada de Fourier é chamada de representação do domínio da frequência do sinal original. O termo transformada de Fourier refere-se à ambas representações do domínio frequência e a operação matemática que associa a representação domínio frequência a uma função temporal. A transformada de Fourier não é limitada a funções temporais, contudo para fins de convenção, o domínio original é comumente referido como domínio do tempo. Para muitas funções de interesse prático, pode-se definir uma operação de reversão: a transformada inversa de Fourier, também chamada de síntese de Fourier, de um domínio de frequência combina as contribuições de todas as frequências diferentes para a reconstituição de uma função temporal original.

Operações lineares aplicadas em um dos domínios(tempo ou frequência) resultam em operações correspondentes no outro domínio, o que, em certas ocasiões, podem ser mais fáceis de efetuar. A operação de diferenciação no domínio do tempo corresponde à multiplicação na frequência, o que torna mais fácil a análise de equações diferenciais no domínio da frequência. Além disso, a convolução no domínio temporal corresponde à multiplicação ordinária no domínio da frequência. Isso significa que qualquer sistema linear que não varia com o tempo, como um filtro aplicado a um sinal, pode ser expressado de maneira relativamente simples como uma operação nas frequências. Após realizar a operação desejada, a transformação do resultado alterna para o domínio do tempo. A Análise harmônica é o estudo sistemático da relação entre os domínios de tempo e frequência, incluindo os tipos de funções ou operações que são mais "simples" em um ou em outro, e possui ligações profundas a muitas áreas da matemática moderna.

Definição |

Diversas notações são convencionadas para denotar a transformação de Fourier de uma função f:R→C{displaystyle mathrm {f:mathbb {R} rightarrow mathbb {C} } }. Utilizaremos a seguinte representação:

f^(ω)≡F(ω)≡F{f(t)} =def∫−∞∞f(t) e−iωtdt     Transformada de Fourier do dominio do tempo {displaystyle mathrm {{hat {f}}(omega )equiv F(omega )equiv {mathcal {F}}{f(t)} {overset {underset {mathrm {def} }{}}{=}}int _{-infty }^{infty }f(t) e^{-iomega t}operatorname {d} !t} {begin{aligned}&{mathsf {Transformada de Fourier }}\&{mathsf {do dominio do tempo }}end{aligned}}}

f(t)≡F−1{F(ω)} =def 12π∫−∞∞F(ω) eiωtdω      ω≡2πf (Freque^ncia angular){displaystyle mathrm {f(t)equiv {mathcal {F}}^{-1}{F(omega )} {overset {underset {mathrm {def} }{}}{=}} {frac {1}{2pi }}int _{-infty }^{infty }F(omega ) e^{iomega t}operatorname {d} !omega omega equiv 2pi f} {mathsf {(Frequ{hat {e}}ncia angular)}}}

f^(κ)≡F(κ)≡F{f(x)} =def∫−∞∞f(x) e−iκxdx     Transformada de Fourier do dominio do espaco {displaystyle mathrm {{hat {f}}(kappa )equiv F(kappa )equiv {mathcal {F}}{f(x)} {overset {underset {mathrm {def} }{}}{=}}int _{-infty }^{infty }f(x) e^{-ikappa x}operatorname {d} !x} {begin{aligned}&{mathsf {Transformada de Fourier }}\&{mathsf {do dominio do espaco }}end{aligned}}}

f(x)≡F−1{F(κ)} =def 12π∫−∞∞F(κ) eiκxdκ     κ≡2πλ (Vetor de onda){displaystyle mathrm {f(x)equiv {mathcal {F}}^{-1}{F(kappa )} {overset {underset {mathrm {def} }{}}{=}} {frac {1}{2pi }}int _{-infty }^{infty }F(kappa ) e^{ikappa x}operatorname {d} !kappa kappa equiv {frac {2pi }{lambda }}} {mathsf {(Vetor de onda)}}}

f{displaystyle mathrm {f} }

f^{displaystyle mathrm {hat {f}} }

f{displaystyle mathrm {f} }

f^{displaystyle mathrm {hat {f}} }

Introdução |

Artigo principal: Análise de Fourier

Uma motivação para a transformada de Fourier vêm do estudo da série de Fourier. Nesse estudo, funções complicadas porém periódicas são escritas como o somatório de ondas simples matematicamente representadas por senos e cossenos. A transformada de Fourier é uma extensão da série de Fourier que resulta quando o período da função representada é maximizado, aproximando-se do infinito.

Nos primeiros quadros, uma função f{displaystyle mathrm {f} } é representada por uma série de Fourier: uma combinação linear de senos e cossenos (em azul). As componentes frequência desses senos e cossenos distribuem-se ao longo do espectro de frequência; são representadas como deltas de Dirac no eixo ω{displaystyle omega }. A representação do domínio da função f^{displaystyle mathrm {hat {f}} } é o conjunto desses picos nas frequências que aparecem na resolução da função.

Devido às propriedades dos senos e dos cossenos, é possível determinar a amplitude de cada onda da série de Fourier utilizando uma integração. Em muitos casos é desejável usar a identidade de Euler, e±i2πϕ≡cos⁡(2πϕ)±isin⁡(2πϕ){displaystyle mathrm {e^{pm i2pi phi }equiv cos(2pi phi )pm isin(2pi phi )} }, para escrever a série de Fourier em termos de ondas básicas ei2πϕ{displaystyle mathrm {e^{i2pi phi }} }. Esse procedimento possui a vantagem de simplificar muitas fórmulas envolvidas e provém uma formulação da série de Fourier que relembra a definição utilizada nesse artigo. Reescrevendo senos e cossenos como exponenciais complexas torna necessário que os coeficientes de Fourier sejam valores complexos. A intepretação usual desse número complexo é que ele fornece ambas amplitude (ou tamanho) da onda presente na função e a fase (ou ângulo inicial) da onda. Essas exponenciais complexas algumas vezes possuem "frequências" negativas. Se ϕ{displaystyle mathrm {phi } } é medido em segundos, então ambas ondas ei2πϕ{displaystyle mathrm {e^{i2pi phi }} } e e−i2πϕ{displaystyle mathrm {e^{-i2pi phi }} } completam um ciclo por segundo mas representam frequências diferentes na transformada de Fourier. Assim, frequência não mais mede o número de ciclos por unidade de tempo, mas ainda possui interpretação similar.

Existe uma forte conexão entre as definições de série de Fourier e a transformada de Fourier para funções f{displaystyle mathrm {f} } que são zero fora de um intervalo. Para tal função, pode-se calcular sua série de Fourier em qualquer intervalo que inclui os pontos onde f{displaystyle mathrm {f} } não é identicamente zero. A transformada de Fourier também é definida para tal função. À medida que aumenta-se o comprimento do intervalo em que calcula-se a série de Fourier, então os coeficientes da série de Fourier começam a assemelhar-se à transformada de Fourier e o somatório da série de Fourier de f{displaystyle mathrm {f} } começa a assemelhar-se à transformada inversa de Fourier. Para explicar isso mais precisamente, suponha que T{displaystyle mathrm {T} } é suficientemente longo que o intervalo [−T2,T2]{displaystyle mathrm {left[-{frac {T}{2}},{frac {T}{2}}right]} } contenha o intervalo em que f{displaystyle mathrm {f} } não seja identicamente zero. Então o n-ésimo termo do coeficiente Cn{displaystyle mathrm {C_{n}} } será dado por

Cn=1T∫−T2T2f(t) e−iωntdt       ωn≡n2πT{displaystyle mathrm {C_{n}={frac {1}{T}}int _{-{frac {T}{2}}}^{frac {T}{2}}f(t) e^{-iomega _{n}t}operatorname {d} !t omega _{n}equiv n{frac {2pi }{T}}} }

Comparando isso com a definição de transformada de Fourier, pode-se deduzir que

Cn=1Tf^(ωn2π)≡1Tf^(nT){displaystyle mathrm {C_{n}={frac {1}{T}}{hat {f}}{Bigl (}{frac {omega _{n}}{2pi }}{Bigr )}equiv {frac {1}{T}}{hat {f}}{Bigl (}{frac {n}{T}}{Bigr )}} }

desde que f{displaystyle mathrm {f} } seja nula fora do intervalo [−T2,T2]{displaystyle mathrm {left[-{frac {T}{2}},{frac {T}{2}}right]} }.

Sob certas condições, a série de Fourier de f{displaystyle mathrm {f} } pode ser igual à função f{displaystyle mathrm {f} }. Em outras palavras, f{displaystyle mathrm {f} } pode ser escrita como

f(t)=∑n=−∞∞Cn eiωnt≡∑n=−∞∞f^(ωn2π) eiωntΔωn2π{displaystyle mathrm {f(t)=sum _{n=-infty }^{infty }C_{n} e^{iomega _{n}t}equiv sum _{n=-infty }^{infty }{hat {f}}{Bigl (}{frac {omega _{n}}{2pi }}{Bigr )} e^{iomega _{n}t}{frac {Delta omega _{n}}{2pi }}} }

onde o segundo somatório é simplesmente o primeiro somatório reescrito, utilizando as definições ωn =def n2πT{displaystyle mathrm {omega _{n} {overset {underset {mathrm {def} }{}}{=}} n{frac {2pi }{T}}} } e Δωn =def n+1T−nT{displaystyle mathrm {Delta omega _{n} {overset {underset {mathrm {def} }{}}{=}} {frac {n+1}{T}}-{frac {n}{T}}} }.

O segundo somatório configura uma soma de Riemann, e à medida em que T→∞{displaystyle mathrm {Trightarrow infty } } ela convergirá para a integral da transformada de Fourier inversa apresentada na seção de Definição.

No estudo da série de Fourier os números Cn{displaystyle mathrm {C_{n}} } podem ser interpretados como a "quantidade" da onda presente na série de Fourier de f{displaystyle mathrm {f} }. Semelhantemente, como visto acima, a transformada de Fourier pode ser vista como a função que mensura o quanto de cada frequência individual encontra-se presente na função f{displaystyle mathrm {f} }, e pode-se recombinar essas ondas com o uso da transformada inversa de Fourier, reproduzindo a função original.

Propriedades da transformada de Fourier |

Assume-se aqui que f(t){displaystyle mathrm {f(t)} },g(t){displaystyle mathrm {g(t)} } e h(t){displaystyle mathrm {h(t)} } são funções integráveis: Lebesgue-mensuráveis no domínio R{displaystyle mathbb {R} } satisfazendo ∫−∞∞|f(t)|dt<∞  .{displaystyle mathrm {int _{-infty }^{infty }|f(t)|operatorname {d} !t<infty .} }

Denota-se as transformadas de Fourier destas funções como f^(ω){displaystyle mathrm {{hat {f}}(omega )} }, g^(ω){displaystyle mathrm {{hat {g}}(omega )} } e h^(ω){displaystyle mathrm {{hat {h}}(omega )} }, respectivamente.

Propriedades básicas |

A transformada de Fourier possui as seguintes propriedades básicas:

∘{displaystyle circ } Linearidade

Para quaisquer números complexos a{displaystyle mathrm {a} } e b{displaystyle mathrm {b} }, se f(t)=a g(t)+b h(t){displaystyle mathrm {f(t)=a g(t)+b h(t)} }, então f^(ω)=a g^(ω)+b h^(ω) .{displaystyle mathrm {{hat {f}}(omega )=a {hat {g}}(omega )+b {hat {h}}(omega )} .}

Demonstração:

Essa demonstração vem direto da propriedade de linearidade da integral.

Seja:
F{f(t)}{displaystyle {mathcal {F}}{f(t)}}=F{a g(t)+b h(t)}{displaystyle {mathcal {F}}{a g(t)+b h(t)}}

=∫−∞∞(a g(t)+b h(t))e−itωdt{displaystyle =int _{-infty }^{infty }(a g(t)+b h(t))e^{-itomega }dt}

=∫−∞∞a g(t)e−itωdt+∫−∞∞b h(t)e−itωdt{displaystyle =int _{-infty }^{infty }a g(t)e^{-itomega }dt+int _{-infty }^{infty }b h(t)e^{-itomega },dt}

=a∫−∞∞g(t)e−itωdt+b∫−∞∞h(t)e−itωdt{displaystyle =aint _{-infty }^{infty }g(t)e^{-itomega },dt+bint _{-infty }^{infty }h(t)e^{-itomega },dt}

=a g^(ω)+b h^(ω){displaystyle =a {hat {g}}(omega )+b {hat {h}}(omega )}

^[2]

∘{displaystyle circ } Translação ou deslocamento no tempo

Para qualquer número real t0{displaystyle mathrm {t_{0}} }, se f(t)=g(t−t0){displaystyle mathrm {f(t)=g(t-t_{0})} }, então f^(ω)=e−iωt0g^(ω) .{displaystyle mathrm {{hat {f}}(omega )=e^{-iomega t_{0}}{hat {g}}(omega )} .}

Demonstração:

F{f(t−t0)}=∫−∞∞f(t−t0)e−iωtdt{displaystyle {mathcal {F}}{f(t-t_{0})}=int _{-infty }^{infty }f(t-t_{0})e^{-iomega t}dt}

Fazendo s=t−t0{displaystyle s=t-t_{0}} e t=s+t0{displaystyle t=s+t_{0}}, obtemos:

F{f(t−t0)}=∫−∞∞f(s)e−iω(s+t0)ds{displaystyle {mathcal {F}}{f(t-t_{0})}=int _{-infty }^{infty }f(s)e^{-iomega (s+t_{0})}ds}

F{f(t−t0)}=∫−∞∞f(s)e−iωse−iωt0ds{displaystyle {mathcal {F}}{f(t-t_{0})}=int _{-infty }^{infty }f(s)e^{-iomega s}e^{-iomega t_{0}}ds}

F{f(t−t0)}=e−iωt0∫−∞∞f(s)e−iωsds{displaystyle {mathcal {F}}{f(t-t_{0})}=e^{-iomega t_{0}}int _{-infty }^{infty }f(s)e^{-iomega s}ds}

F{f(t−t0)}=e−iωt0f^(ω){displaystyle {mathcal {F}}{f(t-t_{0})}=e^{-iomega t_{0}}{hat {f}}(omega )} ^[3]

∘{displaystyle circ } Modulação ou deslocamento na frequência

Para qualquer número real ω0{displaystyle omega _{0}}, se f(t)=eiω0tg(t){displaystyle mathrm {f(t)=e^{iomega _{0}t}g(t)} }, então f^(ω)=g^(ω−ω0) .{displaystyle mathrm {{hat {f}}(omega )={hat {g}}(omega -omega _{0})} .}

Demonstração:

Seja:
F{f(t)}{displaystyle {mathcal {F}}{f(t)}}=F{eitω0g(t)}{displaystyle {mathcal {F}}{e^{itomega _{0}}g(t)}}

=∫−∞∞eitω0g(t)e−itωdt{displaystyle =int _{-infty }^{infty }e^{itomega _{0}}g(t)e^{-itomega },dt}

=∫−∞∞g(t)e−it(ω−ω0)dt{displaystyle =int _{-infty }^{infty }g(t)e^{-it(omega -omega _{0})},dt}

Usando a definição de Transformada de Fourier

=g^(ω−ω0){displaystyle ={hat {g}}(omega -omega _{0})}

^[4]

∘{displaystyle circ } Mudança de escala

Para um número real a{displaystyle mathrm {a} } não-nulo, se f(t)=g(at){displaystyle mathrm {f(t)=g(at)} }, então f^(ω)=1|a|g^(ωa) .{displaystyle mathrm {{hat {f}}(omega )={frac {1}{|a|}}{hat {g}}{Bigl (}{frac {omega }{a}}{Bigr )}} .} O caso a=−1{displaystyle mathrm {a=-1} } leva à propriedade da inversão temporal, a qual afirma: se g(t)=h(−t){displaystyle mathrm {g(t)=h(-t)} }, então g^(ω)=h^(−ω) .{displaystyle mathrm {{hat {g}}(omega )={hat {h}}(-omega )} .}

Demonstração:

Seja F{f(at)}{displaystyle {mathcal {F}}{f(at)}} =∫−∞∞f(at)e−itωdt{displaystyle =int _{-infty }^{infty }f(at)e^{-itomega },dt}

Fazendo uma mudança de variável onde τ=at{displaystyle tau =at}, temos:

∫−∞∞f(τ)e−iτωadτa{displaystyle int _{-infty }^{infty }f(tau )e^{frac {-itau omega }{a}},{frac {dtau }{a}}}

Caso 1: a>0{displaystyle a>0}

Chamando a{displaystyle a} de |a|{displaystyle |a|}

=1|a|∫−∞∞f(τ)e−iτω|a|dτ{displaystyle ={frac {1}{|a|}}int _{-infty }^{infty }f(tau )e^{frac {-itau omega }{|a|}},dtau }

=1|a|g^(ω|a|){displaystyle ={frac {1}{|a|}}{hat {g}}{Bigl (}{frac {omega }{|a|}}{Bigr )}}

Caso 2: a<0{displaystyle a<0}

Chamando agora a{displaystyle a} de −|a|{displaystyle -|a|}

=1−|a|∫∞−∞f(τ)e−iτω−|a|dτ{displaystyle ={frac {1}{-|a|}}int _{infty }^{-infty }f(tau )e^{frac {-itau omega }{-|a|}},dtau }

Trocando τ{displaystyle tau } por −τ{displaystyle -tau }

=1−|a|∫−∞∞f(−τ)e−iτω|a|d(−τ){displaystyle ={frac {1}{-|a|}}int _{-infty }^{infty }f(-tau )e^{frac {-itau omega }{|a|}},d(-tau )}

=1|a|∫−∞∞f(−τ)e−iτω|a|d(τ){displaystyle ={frac {1}{|a|}}int _{-infty }^{infty }f(-tau )e^{frac {-itau omega }{|a|}},d(tau )}

Usando a propriedade da inversão temporal:

1|a|g^(−ω|a|){displaystyle {frac {1}{|a|}}{hat {g}}{Bigl (}{frac {-omega }{|a|}}{Bigr )}}

Ou seja, em todos os casos:

F{f(at)}{displaystyle {mathcal {F}}{f(at)}} =1|a|g^(ωa){displaystyle ={frac {1}{|a|}}{hat {g}}{Bigl (}{frac {omega }{a}}{Bigr )}}^[5]

∘{displaystyle circ } Conjugação

Se f(t)=g(t)¯{displaystyle mathrm {f(t)={overline {g(t)}}} }, então f^(ω)=g^(−ω)¯{displaystyle mathrm {{hat {f}}(omega )={overline {{hat {g}}(-omega )}}} } ou f^(−ω)=g^(ω)¯ .{displaystyle mathrm {{hat {f}}(-omega )={overline {{hat {g}}(omega )}}} .}

Em particular, se R∋f{displaystyle mathbb {R} ni mathrm {f} }, têm-se a condição de realidade g^(−ω)=g^(ω)¯{displaystyle mathrm {{hat {g}}(-omega )={overline {{hat {g}}(omega )}}} }, ou seja, f{displaystyle mathrm {f} } é uma função Hermitiana.

Por outro lado, se f{displaystyle mathrm {f} } é puramente imaginária então g^(−ω)=−g^(ω)¯ .{displaystyle mathrm {{hat {g}}(-omega )=-{overline {{hat {g}}(omega )}}} .}

∘{displaystyle circ } Integração^[6]

Substituindo ω=0{displaystyle mathrm {omega =0} } na definição, obtém-se que f^(0)=∫−∞∞f(t) dt{displaystyle mathrm {{hat {f}}(0)=int _{-infty }^{infty }f(t) dt} }, ou seja, a avaliação da transformada de Fourier na origem corresponde à integral de f{displaystyle mathrm {f} } sobre todo o eixo.

Assim, F{∫−∞tf(τ)dτ}=1iωF(ω){displaystyle mathrm {{mathcal {F}}{int _{-infty }^{t}f(tau )dtau }={frac {1}{iomega }}F(omega )} }, onde f(t){displaystyle mathrm {f(t)} } é uma função integrável tal que sua transformada de Fourier f^(ω){displaystyle mathrm {{hat {f}}(omega )} } satisfaça f^(0)=0 .{displaystyle mathrm {{hat {f}}(0)=0 .} }

Simetria e Dualidade |

Muitas vezes não se pensa em nenhuma unidade como sendo anexada às duas variáveis ​​t e ξ. Mas em aplicações físicas, ξ deve ter unidades inversas às unidades de t. Por exemplo, se t é medido em segundos, ξ deve ser em frequência, para que as fórmulas mostradas aqui sejam válidas. Se a escala de t é alterada e t é medido na unidades de 2π segundos, então ξ deve estar na chamada "frequência angular", ou deve-se inserir algum fator de escala constante em algumas das fórmulas. Se t é medido em unidades de comprimento, ξ deve estar no comprimento inverso. Isto e para afirmar que existem duas cópias da linha real: uma medida em um conjunto de unidades, onde t varia, e outra em unidades inversas às unidades de t, e qual é o intervalo de ξ. Então, essas são duas cópias distintas da linha real e não podem ser identificadas umas com as outras. Portanto, a transformada de Fourier vai de um espaço de funções para um espaço diferente de funções: funções que têm um domínio diferente de definição.

Em geral, ξ deve ser sempre tomado como uma forma linear no espaço de ts, o que equivale a dizer que a segunda linha real é o espaço dual da primeira linha real. Veja o artigo sobre álgebra linear para uma explicação mais formal e para mais detalhes. Este ponto de vista torna-se essencial nas generalizações da transformada de Fourier para grupos gerais de simetria, incluindo o caso das séries de Fourier.

Que não existe uma maneira preferida (muitas vezes, diz-se "não canônico") para comparar as duas cópias da linha real que estão envolvidas na transformada de Fourier - fixar as unidades em uma linha não força a escala das unidades em a outra linha - é a razão para a multiplicidade de convenções rivais sobre a definição da transformada de Fourier. As várias definições resultantes de diferentes escolhas de unidades diferem por várias constantes

Dada uma funcao f(t) e sua transformada F(w) então :

f(−ω)=12πF{F(t)}{displaystyle f(-omega )={frac {1}{2pi }}{mathcal {F}}{F(t)}}

como antes, porem a alternativa correspondente a inversão da equação deve ser:

f(t)=12π∫−∞∞F(ω)eitωdω.{displaystyle f(t)={frac {1}{2pi }}int _{-infty }^{infty }F(omega )e^{itomega },domega .}

Para se obter uma equação com a frequência angular mas mais simetrica entre a transformada de Fourier e a equação de inversão.Comumente se a usa alternativa da transformada de Fourier, com o fator 2π{displaystyle {sqrt {2pi }}} logo:

F(ω)=12π∫−∞∞f(t)e−iωtdt,{displaystyle {mathcal {F}}(omega )={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }f(t)e^{-iomega t},dt,}

e a equação de inversão correspondente:

f(t)=12π∫−∞∞F(ω)eitωdω.{displaystyle f(t)={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }{mathcal {F}}(omega )e^{itomega },domega .}

Em algumas convenções incomuns, como aquelas empregadas pelo comando FourierTransform da Wolfram Language, a transformada de Fourier tem i no expoente em vez de −i, e vice-versa para a fórmula de inversão. Muitas das identidades que envolvem a transformada de Fourier permanecem válidas naquelas convenções, desde que todos os termos que explicitamente envolvem a substituam por −i.

Por exemplo, na teoria da probabilidade, a função característica ϕ da função de densidade de probabilidade f de uma variável aleatória X de tipo contínuo é definida sem um sinal negativo no exponencial e, como as unidades de x são ignoradas, não há 2π:

ϕ(λ)=∫−∞∞f(x)eiλxdx.{displaystyle phi (lambda )=int _{-infty }^{infty }f(x)e^{ilambda x},dx.}

(Na teoria das probabilidades, e na estatística matemática, o uso da transformada de Fourier-Stieltjes é preferido, porque muitas variáveis ​​aleatórias não são do tipo contínuo, e não possuem uma função de densidade, e é preciso tratar funções de distribuição descontínuas, ou seja, medidas que possuem "átomos".

Do ponto de vista mais elevado dos caracteres do grupo, que é muito mais abstrato, todas essas escolhas arbitrárias desaparecem, como será explicado na seção posterior deste artigo, sobre a noção da transformada de Fourier de uma função em um grupo local compacto abeliano. .

Continuidade uniforme e o lema de Riemann-Labesgue |

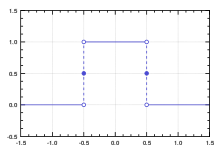
A função retangular e uma integral de Lebesgue

A transformada de Fourier pode ser definida em alguns casos para funções não integráveis, mas as transformadas de Fourier de funções integráveis ​​possuem várias propriedades fortes.

A transformada de Fourier f̂ de qualquer função integrável f é uniformemente contínua e^[7]

‖f^‖∞≤‖f‖1{displaystyle left|{hat {f}}right|_{infty }leq left|fright|_{1}}

Pelo lema de Riemann-Labesgue:^[8]

f^(ξ)→0 as |ξ|→∞.{displaystyle {hat {f}}(xi )to 0{text{ as }}|xi |to infty .}

No entanto, f^{displaystyle {hat {f}}} não precisa ser integrável. Por exemplo, a transformada de Fourier da função retangular, que é integrável, é a função sinc, que não é integrável de Lebesgue, porque suas integrais impróprias se comportam analogamente à série harmônica alternada, convergindo para uma soma sem ser absolutamente convergente. Geralmente não é possível escrever a transformada inversa como uma integral de Lebesgue. No entanto, quando f e f^{displaystyle {hat {f}}} são integráveis, a igualdade inversa

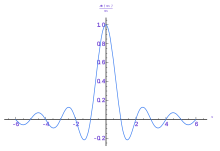
A função Sinc , que e a transformada da função retangular, e fixa e continua mas não e uma integral de Lebesgue.

f(x)=∫−∞∞f^(ξ)e2iπxξdξ{displaystyle f(x)=int _{-infty }^{infty }{hat {f}}(xi )e^{2ipi xxi },dxi }

mantém quase todos os lugares. Ou seja, a transformada de Fourier é injetiva em L¹(ℝ). (Mas se f é contínuo, então a igualdade vale para todo x.)

Teorema de Plancherel e Teorema de Parseval |

Artigos principais: Dualidade de Pontryagin, Teorema de Plancherel e Teorema de Parseval.

Sejam f(t){displaystyle mathrm {f(t)} } e g(t){displaystyle mathrm {g(t)} } integráveis e f^(ω){displaystyle mathrm {{hat {f}}(omega )} } e g^(ω){displaystyle mathrm {{hat {g}}(omega )} } suas respectivas transformadas de Fourier. Se os quadrados de f(t){displaystyle mathrm {f(t)} } e g(t){displaystyle mathrm {g(t)} } sejam integráveis, então temos a fórmula de Parseval:

∫−∞∞f(t) g(t)¯ dt=∫−∞∞f^(ω) g^(ω)¯ dω{displaystyle mathrm {int _{-infty }^{infty }f(t) {overline {g(t)}} dt=int _{-infty }^{infty }{hat {f}}(omega ) {overline {{hat {g}}(omega )}} domega } }

onde g(t)¯{displaystyle {overline {mathrm {g(t)} }}} e g^(ω)¯{displaystyle mathrm {overline {{hat {g}}(omega )}} } são conjugados complexos.

O teorema de Plancherel, que segue o princípio acima, afirma que ∫−∞∞|f(t)|2dt=12π∫−∞∞|f^(ω)|2dω .{displaystyle mathrm {int _{-infty }^{infty }|f(t)|^{2}dt={frac {1}{2pi }}int _{-infty }^{infty }|{hat {f}}(omega )|^{2}domega } .}

Diferenciação |

Suponha que f{displaystyle mathrm {f} } seja uma função diferenciável e ambas f{displaystyle mathrm {f} } e sua derivada f′{displaystyle mathrm {f'} } são integráveis. Então a transformada de Fourier da derivada é dada por

f′^(ω)=iωf^(ω) .{displaystyle mathrm {{widehat {f'}}(omega )=iomega {hat {f}}(omega )} .}

Demonstração:

F{f′(t)}=∫−∞∞f′(t)e−iωtdt{displaystyle {mathcal {F}}{f'(t)}=int _{-infty }^{infty }f'(t)e^{-iomega t}dt}

Por Integração por partes, obtemos:

F{f′(t)}=[f(t)e−iωt]−∞∞−∫−∞∞−iωf(t)e−iωtdt{displaystyle {mathcal {F}}{f'(t)}={big [}f(t)e^{-iomega t}{big ]}_{-infty }^{infty }-int _{-infty }^{infty }-iomega f(t)e^{-iomega t}dt}

Tendo que:

limt→±∞f(t)=0{displaystyle lim _{tto pm infty }f(t)=0}

F{f′(t)}=iω∫−∞∞f(t)e−iωtdt{displaystyle {mathcal {F}}{f'(t)}=iomega int _{-infty }^{infty }f(t)e^{-iomega t}dt}

F{f′(t)}=iωf^(ω){displaystyle {mathcal {F}}{f'(t)}=iomega {hat {f}}(omega )}

Mais amplamente, a transformada de Fourier da n-ésima derivada f(n){displaystyle mathrm {f^{(n)}} } é dada por

f(n)^(ω)=(iω)nf^(ω) .{displaystyle mathrm {{widehat {f^{(n)}}}(omega )=(iomega )^{n}{hat {f}}(omega )} .}

Ao aplicar a transformada de Fourier e utilizar tais propriedades, algumas equações diferenciais ordinárias podem ser transformadas em equações algébricas, que possuem complexidade reduzida. Estas propriedades também implicam que "f{displaystyle mathrm {f} } é suave se, e somente se, f^{displaystyle mathrm {hat {f}} } decai rapidamente para 0{displaystyle mathrm {0} } quando |ω|→∞{displaystyle |omega |rightarrow infty }". Utilizando a regra análoga para a transformada inversa de Fourier, pode-se dizer que "f{displaystyle mathrm {f} } decai rapidamente para 0{displaystyle mathrm {0} } quando |t|→∞{displaystyle mathrm {|t|rightarrow infty } } se, e somente se, f^{displaystyle mathrm {hat {f}} } é suave".

Derivada da transformada |

indndωnF{f(t)}=F{tn f(t)}{displaystyle mathrm {i^{n}{frac {d^{n}}{domega ^{n}}}{mathcal {F}}left{f(t)right}={mathcal {F}}left{t^{n} f(t)right}} }^[9]

Teorema da Convolução |

A transformada de Fourier translada entre convolução e multiplicação de funções. Se g(t){displaystyle mathrm {g(t)} } e h(t){displaystyle mathrm {h(t)} } são funções integráveis com as transformadas de Fourier g^(ω){displaystyle mathrm {{hat {g}}(omega )} } e h^(ω){displaystyle mathrm {{hat {h}}(omega )} }, respectivamente, então a transformada de Fourier da convolução é dada pelo produto das transformadas de Fourier g^(ω){displaystyle mathrm {{hat {g}}(omega )} } e h^(ω){displaystyle mathrm {{hat {h}}(omega )} }.

Isso significa que, se

f(t)=g(t)∗h(t)=∫−∞∞g(ν)h(t−ν)dν{displaystyle mathrm {f(t)=g(t)*h(t)=int _{-infty }^{infty }g(nu )h(t-nu )dnu } }

então

f^(ω)=g^(ω)⋅h^ .{displaystyle mathrm {{hat {f}}(omega )={hat {g}}(omega )cdot {hat {h}}} .}

Em sistemas lineares invariantes no tempo, é comum interpretar h(t){displaystyle mathrm {h(t)} } como a resposta ao impulso do sistema com g(t){displaystyle mathrm {g(t)} } como entrada e f(t){displaystyle mathrm {f(t)} } como a saída, já que substituindo a unidade de impulso por g(t){displaystyle mathrm {g(t)} } obtém-se f(t)=h(t){displaystyle mathrm {f(t)=h(t)} }. Neste caso, h^(ω){displaystyle mathrm {{hat {h}}(omega )} } representa a frequência de resposta do sistema.

Fenômeno de Gibbs |

Fenômeno de Gibbs : Análise de Fourier: Um Livro Colaborativo

A convergência das somas parciais da série de Fourier de uma função suave por partes em torno de um salto apresenta oscilações cujas amplitudes não convergem para zero. A convergência ponto a ponto acontece, no entanto ao analisar o valor absoluto da diferença entre a função e a soma parcial tem-se que o valor é aproximadamente 8,9% da amplitude do salto.

Se f(t){displaystyle mathrm {f(t)} } é T-periódico e suave por partes e possui uma descontinuidade por salto, então MAX|f(t)−fN(t)|≈8.9%{displaystyle mathrm {MAX{Bigg |}f(t)-f_{N}(t){Bigg |}thickapprox 8.9%} } da amplitude do salto, onde t∈[0,T]{displaystyle mathrm {tin [0,T]} } e

fN(t)=a02+∑n=1Nan cos(ωnt)+∑n=1Nbn sin(ωnt) .{displaystyle mathrm {f_{N}(t)={frac {a_{0}}{2}}+sum _{n=1}^{N}a_{n} cos(omega _{n}t)+sum _{n=1}^{N}b_{n} sin(omega _{n}t) .} }

Esse fenômeno é chamado de Fenômeno de Gibbs^[10].

Diagramas de Espectro |

Diagrama de espectro da transformada de Fourier é a representação gráfica da transformada de Fourier G(ω){displaystyle mathrm {G(omega )} }associadas a uma função g(t){displaystyle mathrm {g(t)} }. Da mesma forma como o diagrama de espectro da série de Fourier se divide em amplitude e fase, o diagrama de espectro da transformada de Fourier se divide em magnitude e em fase. Ou seja, o gráfico de |G(ω)|{displaystyle mathrm {|G(omega )|} }e a diagrama de Magnitude e o gráfico de ϕ(ω){displaystyle mathrm {phi (omega )} }e o diagrama de fase, onde G(ω)=|G(ω)|eiϕ(ω) .{displaystyle mathrm {G(omega )=|G(omega )|e^{iphi (omega )} .} }

Diagrama espectro de magnitude da transformada de Fourier de uma sinal f(t) .{displaystyle mathrm {f(t) .} }

Diagrama de magnitude de g(t)=f(t) cos(400t) .{displaystyle mathrm {g(t)=f(t) cos(400t) .} }

Simetria e paridade |

O par de funções f(t){displaystyle mathrm {f(t)} }e f^(ω){displaystyle mathrm {{hat {f}}(omega )} }exibem propriedades interessantes com relação à simetria e à paridade. Por exemplo, se f(t){displaystyle mathrm {f(t)} }for uma função par, f^(ω){displaystyle mathrm {{hat {f}}(omega )} }também o é. Essas propriedades muitas vezes ajudam na análise e inclusive no cálculo da transformada. Por exemplo, se f(t){displaystyle mathrm {f(t)} }for par, o intervalo de integração pode ser alterado para [0, ∞]{displaystyle [0, infty ]}em lugar de [−∞, ∞]{displaystyle [-infty , infty ]}, dobrando-se o valor calculado da integral. Algumas relações importantes estão listadas na tabela abaixo.

Simetria dos pares de Fourier^[11]

f(t){displaystyle mathrm {f(t)} }	f^(ω){displaystyle mathrm {{hat {f}}(omega )} }
Par	Par
Ímpar	Ímpar
Real e par	Real e par
Real e ímpar	Imaginária e ímpar
Imaginária e par	Imaginária e par
Complexa e par	Complexa e par
Complexa e ímpar	Complexa e ímpar
Real e assimétrica	Hermitiana[nota 1]
Imaginária e assimétrica	Anti-hermitiana[nota 2]
Hermitiana[nota 1]	Real
Anti-hermitiana[nota 2]	Imaginária

Outro tipo de simetria relaciona-se ao conjugado complexo de f(t){displaystyle mathrm {f(t)} }, denotado por f(t)¯{displaystyle mathrm {overline {f(t)}} }, que só tem significado quando t{displaystyle mathrm {t} }é um número complexo. Se denotarmos a transformada de Fourier de f(t){displaystyle mathrm {f(t)} }por f^(ω){displaystyle mathrm {{hat {f}}(omega )} }, a transformada de f(t)¯{displaystyle mathrm {overline {f(t)}} } será denotada por f^(−ω)¯{displaystyle mathrm {overline {{hat {f}}(-omega )}} }, ou seja, a reflexão com relação ao eixo ω{displaystyle omega }do conjugado de f^(ω){displaystyle mathrm {{hat {f}}(omega )} }. Os casos de interesse aparecem na tabela abaixo.

Relação dos conjugados dos pares de Fourier^[12]

f(t){displaystyle mathrm {f(t)} }	f^(−ω)¯{displaystyle mathrm {overline {{hat {f}}(-omega )}} }
Real	f^(ω){displaystyle mathrm {{hat {f}}(omega )} }
Imaginária	−f^(ω){displaystyle mathrm {-{hat {f}}(omega )} }
Par	f^(ω)¯{displaystyle mathrm {overline {{hat {f}}(omega )}} }
Ímpar	−f^(ω)¯{displaystyle mathrm {-{overline {{hat {f}}(omega )}}} }

A tabela abaixo apresenta propriedades interessantes a partir dos fatos das duas tabelas anteriores.

Propriedades dos conjugados dos pares de Fourier^[13]

f(t){displaystyle mathrm {f(t)} }	f^(ω){displaystyle mathrm {{hat {f}}(omega )} }
f(t){displaystyle mathrm {f(t)} }	f^(ω){displaystyle mathrm {{hat {f}}(omega )} }
f(t)¯{displaystyle mathrm {overline {f(t)}} }	f^(−ω)¯{displaystyle mathrm {overline {{hat {f}}(-omega )}} }
f(−t)¯{displaystyle mathrm {overline {f(-t)}} }	f^(ω)¯{displaystyle mathrm {overline {{hat {f}}(omega )}} }
f(−t){displaystyle mathrm {f(-t)} }	f^(−ω){displaystyle mathrm {{hat {f}}(-omega )} }
ℜ[ f(t) ]{displaystyle Re [mathrm { f(t) } ]}	f^(ω)+f^(−ω)¯2{displaystyle mathrm {frac {{hat {f}}(omega )+{overline {{hat {f}}(-omega )}}}{2}} }
ℑ[ f(t) ]{displaystyle Im [mathrm { f(t) } ]}	f^(ω)−f^(−ω)¯2{displaystyle mathrm {frac {{hat {f}}(omega )-{overline {{hat {f}}(-omega )}}}{2}} }
f(t)+f(−t)¯{displaystyle mathrm {f(t)+{overline {f(-t)}}} }	2⋅ℜ[ f^(ω) ]{displaystyle 2cdot Re [ mathrm {{hat {f}}(omega )} ]}
f(t)−f(−t)¯{displaystyle mathrm {f(t)-{overline {f(-t)}}} }	2⋅ℑ[ f^(ω) ]{displaystyle 2cdot Im [ mathrm {{hat {f}}(omega )} ]}
Onde: ℜ[ f(t) ]{displaystyle Re [mathrm { f(t) } ]}é a parte Real de f(t) .{displaystyle mathrm {f(t) .} } ℑ[ f(t) ]{displaystyle Im [mathrm { f(t) } ]}é a parte Imaginária de f(t) .{displaystyle mathrm {f(t) .} }

Aplicações |

Análise de equações diferenciais parciais |

Talvez a a aplicação de maior importância da transformada de Fourier seja a resolução de equações diferenciais parciais. Muitas das equações da física matemática do século XIX podem ser tratadas desta maneira. Fourier estudou a equação do calor, a qual em uma dimensão é

∂2y(x,t)∂x2=∂y(x,t)∂t .{displaystyle mathrm {{partial ^{2}y(x,t) over partial x^{2}}={partial y(x,t) over partial t}} .}

Contudo, daremos um exemplo de dificuldade levemente maior, a equação da onda em uma dimensão,

∂2y(x,t)∂x2=∂2y(x,t)∂t2 .{displaystyle mathrm {{partial ^{2}y(x,t) over partial x^{2}}={partial ^{2}y(x,t) over partial t^{2}}} .}

Aqui, o problema não resume-se a achar uma solução: existem infinitas. A dificuldade reside no chamado "problema de contorno": encontrar uma solução que satisfaça as "condições de contorno"

y(x,0)=f(x);    ∂y(x,0)∂t=g(x) .{displaystyle mathrm {y(x,0)=f(x); {partial y(x,0) over partial t}=g(x) .} }

Aqui, f(t){displaystyle mathrm {f(t)} } e g(t){displaystyle mathrm {g(t)} } não são funções fornecidas. Para a equação do calor, apenas uma condição de contorno pode ser fornecida(geralmente a primeira). Porém, para a equação da onda, existem infinitas soluções y(x,t){displaystyle mathrm {y(x,t)} } que satisfazem a primeira condição de contorno. Contudo, quando as duas condições são impostas, existe apenas uma solução possível.

A dificuldade de encontrar a transformada de Fourier y^{displaystyle mathrm {hat {y}} } da solução consiste uma tarefa muito mais simples do que procurar a solução diretamente. Isso acontece porque a transformação gera produtos a partir de diferenciação, e portanto uma equação diferencial parcial aplicada à solução original é transformada em multiplicação por funções polinomiais de duas variáveis aplicada à função transformada. Depois que y^{displaystyle mathrm {hat {y}} } é determinada, pode-se aplicar a transformada inversa de Fourier com a finalidade de encontrar y(x,t){displaystyle mathrm {y(x,t)} }.

Utilizando a notação

Y(κ,t)=y^(κ,t)Y(κ,0)=f^(κ)ddtY(κ,0)=g^(κ){displaystyle {begin{aligned}&mathrm {Y(kappa ,t)={hat {y}}(kappa ,t)} \&mathrm {Y(kappa ,0)={hat {f}}(kappa )} \&mathrm {{frac {d}{dt}}Y(kappa ,0)={hat {g}}(kappa )} end{aligned}}}

e tomando a transformada de Fourier da equação, temos

d2dt2Y(κ,t)+c2κ2Y(κ,t)=0Y(κ,0)=F(κ)ddtY(κ,0)=G(κ){displaystyle {begin{aligned}&mathrm {{frac {d^{2}}{dt^{2}}}Y(kappa ,t)+c^{2}kappa ^{2}Y(kappa ,t)=0} \&mathrm {Y(kappa ,0)=F(kappa )} \&mathrm {{frac {d}{dt}}Y(kappa ,0)=G(kappa )} end{aligned}}}

A solução é dada em termos de senos e cossenos:

Y=Acos(cκt)+Bsin(cκt){displaystyle mathrm {Y=Acos(ckappa t)+Bsin(ckappa t)} }

Impondo as condições de contorno, tem-se

Y(0)=A=F(κ)ddtY(0)=cκB=G(κ){displaystyle {begin{aligned}&mathrm {Y(0)=A=F(kappa )} \&mathrm {{frac {d}{dt}}Y(0)=ckappa B=G(kappa )} end{aligned}}}

Portanto,

Y=F(κ)cos(cκt)+G(κ)cκsin(cκt)≡F(κ)(eicκt+e−icκt)2+G(κ)cκ(eicκt−e−icκt)2i .{displaystyle mathrm {Y=F(kappa )cos(ckappa t)+{frac {G(kappa )}{ckappa }}sin(ckappa t)equiv F(kappa ){frac {(e^{ickappa t}+e^{-ickappa t})}{2}}+{frac {G(kappa )}{ckappa }}{frac {(e^{ickappa t}-e^{-ickappa t})}{2i}}} .}

Tomando a transformada inversa de Fourier, obtém-se

y(x,t)=12(12π∫−∞∞F(κ)(eiκ(x+ct)+eiκ(x−ct))dκ)+12c(12π∫−∞∞G(κ)iκ(eiκ(x+ct)−eiκ(x−ct))dκ) .{displaystyle mathrm {y(x,t)={frac {1}{2}}{biggl (}{frac {1}{2pi }}int _{-infty }^{infty }F(kappa )(e^{ikappa (x+ct)}+e^{ikappa (x-ct)})dkappa {biggr )}+{frac {1}{2c}}{biggl (}{frac {1}{2pi }}int _{-infty }^{infty }{frac {G(kappa )}{ikappa }}(e^{ikappa (x+ct)}-e^{ikappa (x-ct)})dkappa {biggr )}} .}

Sabe-se que

f(x±ct)=12π∫−∞∞F(κ)eiκ(x±ct)dκg(x)=12π∫−∞∞G(κ)eiκxdκe∫x−ctx+ctg(ι)dι=12π∫−∞∞G(κ)iκ(eiκ(x+ct)−eiκ(x−ct))dκ{displaystyle {begin{aligned}&mathrm {f(xpm ct)={frac {1}{2pi }}int _{-infty }^{infty }F(kappa )e^{ikappa (xpm ct)}dkappa } \&mathrm {g(x)={frac {1}{2pi }}int _{-infty }^{infty }G(kappa )e^{ikappa x}dkappa } \&e\&mathrm {int _{x-ct}^{x+ct}g(iota )diota ={frac {1}{2pi }}int _{-infty }^{infty }{frac {G(kappa )}{ikappa }}(e^{ikappa (x+ct)}-e^{ikappa (x-ct)})dkappa } end{aligned}}}

Finalmente,

y(x,t)=f(x+ct)2+f(x−ct)2+12c∫x−ctx+ctg(ι)dι .{displaystyle mathrm {y(x,t)={frac {f(x+ct)}{2}}+{frac {f(x-ct)}{2}}+{frac {1}{2c}}int _{x-ct}^{x+ct}g(iota )diota } .}^[14]

Espectroscopia |

A transformada de Fourier também é utilizada em ressonância magnética nuclear e em outras tipos de espectroscopia, como a infravermelha. Na ressonância magnética nuclear um sinal de decaimento livre induzido em forma exponencial é adquirido no domínio do tempo e Fourier-transformado em uma linha com forma Lorentziana no domínio da frequência. A transformada de Fourier também é aplicada na ressonância magnética por imagem e em espectroscopia de massas.

Mecânica quântica |

A transformada de Fourier é útil na Mecânica Quântica de duas maneiras diferentes. Para começar, a Mecânica Quântica postula a existência de pares de variáveis complementares, ligados pelo princípio da incerteza de Heisenberg. Por exemplo, em uma dimensão, a variável espacial q de uma partícula, pode ser apenas medida pelo "operador de posição" à custa de perda de informações sobre o momento p{displaystyle mathrm {p} } da partícula. Portanto, o estado físico da partícula pode ser descrita por uma função, chamada "função de onda", de q{displaystyle mathrm {q} } ou por uma função de p{displaystyle mathrm {p} }, mas não por uma função de duas variáveis. A variável p{displaystyle mathrm {p} } é chamada de variável conjugada de q{displaystyle mathrm {q} }. Na Mecânica Clássica, o estado físico de uma partícula (existente em uma dimensão, para simplificação) seria dada atribuindo valores para ambos p{displaystyle mathrm {p} } e q{displaystyle mathrm {q} } simultaneamente. Assim, o conjunto de todos os estados físicos possíveis é o espaço vetorial real, bidimensional com um eixo-p{displaystyle mathrm {p} } e um eixo-q{displaystyle mathrm {q} }.

Em contraste, a mecânica quântica escolhe uma polarização do espaço escolhendo um subespaço de metade da dimensão, por exemplo, o eixo-q{displaystyle mathrm {q} }, mas em vez de se considerar apenas os pontos, converte o conjunto de todas as "funções de onda" complexas sobre esse eixo. No entanto, a escolha do eixo-p{displaystyle mathrm {p} } é uma polarização igualmente válida, obtendo-se uma representação diferente do conjunto de possíveis estados físicos da partícula que está relacionada com a primeira representação pela transformação de Fourier.

ϕ(p)=∫ψ(q)e2πipqhdq.{displaystyle mathrm {phi (p)=int psi (q)e^{2pi ipq over h}dq.} }

Fisicamente estados de realização são L2{displaystyle L^{2}} e assim pelo teorema Plancherel, suas transformadas de Fourier também são L2{displaystyle L^{2}}. (Nota-se que desde que q{displaystyle mathrm {q} } é em unidades de distância e p{displaystyle mathrm {p} } está em unidades de força, a presença da constante de Planck no expoente faz com que o expoente seja adimensional, como deve ser.)

Portanto, a transformada de Fourier pode ser utilizada para passar de um modo de representar o estado da partícula, por uma função posição de onda, para uma outra maneira de representar o estado da partícula: por uma função de impulso de onda. Há infinitas maneiras de polarizações possíveis, e todas são igualmente válidas. Ser capaz de transformar estados de uma representação para outra às vezes é conveniente.

O outro uso da transformada de Fourier na mecânica quântica e na teoria quântica de campos é resolver a equação de onda aplicável. Na mecânica quântica não-relativística, a equação de Schrödinger para uma função de onda variável no tempo em uma dimensão, não sujeita a forças externas, é

∂2∂x2ψ(x,t)=ih2π∂∂tψ(x,t).{displaystyle mathrm {{partial ^{2} over partial x^{2}}psi (x,t)=i{frac {h}{2pi }}{partial over partial t}psi (x,t).} }

Esta equação é a mesma para a equação do calor, exceto pela presença da unidade imaginária i . Os métodos de Fourier podem ser utilizados para resolver esta equação.

Na presença de um potencial, determinado pela função de energia potencial V(x){displaystyle mathrm {V(x)} } a equação torna-se

∂2∂x2ψ(x,t)+V(x)ψ(x,t)=ih2π∂∂tψ(x,t).{displaystyle mathrm {{partial ^{2} over partial x^{2}}psi (x,t)+V(x)psi (x,t)=i{frac {h}{2pi }}{partial over partial t}psi (x,t).} }

As "soluções elementares", são os chamadas "estados estacionários " da partícula, e o algoritmo de Fourier, ainda pode ser usado para resolver o problema de contorno da evolução ψ{displaystyle psi } dado os seus valores em t=0{displaystyle mathrm {t=0} }. Nenhuma destas abordagens é de uso muito prático em Mecânica Quântica. Problemas de contorno e a evolução do tempo de uma função de onda não é de grande interesse prático: são os estados estacionários os mais importantes.

Na mecânica quântica relativística, a equação de Schrödinger torna-se uma equação de onda comum na física clássica, a não ser que as ondas de valores complexos sejam consideradas. Um exemplo simples, na ausência de interações com outras partículas ou campos, é a equação unidimensional livre de Klein - Gordon - Schroedinge - Fock , desta vez em unidades adimensionais.

(∂2∂x2+1)ψ(x,t)=∂2∂t2ψ(x,t).{displaystyle mathrm {left({partial ^{2} over partial x^{2}}+1right)psi (x,t)={partial ^{2} over partial t^{2}}psi (x,t).} }

Essa é, do ponto de vista matemático, a mesma que a equação de onda da física clássica resolvida acima (mas com uma onda de valor complexo, que não faz qualquer diferença nos métodos). Isto é de grande utilidade na teoria quântica de campos: cada componente separado de Fourier de uma onda pode ser tratado como um oscilador harmônico separado e, em seguida, quantificado. Procedimento conhecido como "segunda quantização”. Métodos de Fourier foram adaptadas para lidar também com interações não-triviais.

Processamento de sinais |

A transformada de Fourier é aplicada para a análise espectral de séries temporais. O sujeito de processamento estatístico de sinal geralmente não aplica-se, contudo, a transformação de Fourier ao sinal em si. Mesmo se o sinal real é de fato transiente, têm sido encontrado em recomendação prática modelar o sinal por uma função (ou, alternativamente, um processo Estocástico) que é estacionário no sentido que suas propriedades características são constantes no eixo temporal. A transformada de Fourier de tal função não existe no sentido usual, e têm encontrado-se mais útil para a análise de sinais do que aplicar a transformada de Fourier de sua função autocorrelata.

A autocorrelação R{displaystyle mathrm {R} } de uma função f{displaystyle mathrm {f} } é definida por

Rf(τ)=limT→∞12T∫−TTf(t) f(t+τ) dt .{displaystyle mathrm {R_{f}(tau )=lim _{Trightarrow infty }{frac {1}{2T}}int _{-T}^{T}f(t) f(t+tau ) dt .} }

Esta função é uma função do atraso de tempo τ{displaystyle tau } decorre entre os valores de f{displaystyle mathrm {f} } a serem correlacionados.

Para muitas funções f{displaystyle mathrm {f} } que ocorrem na prática, R{displaystyle mathrm {R} } é uma função par do atraso de tempo τ{displaystyle tau } e para típicos sinais que possuem ruídos ela é uniformemente contínua com um máximo em τ=0{displaystyle mathrm {tau =0} }.

A função autocorrelação, mais apropriadamente chamada de função de autocovariância a não ser que seja normalizada de alguma maneira apropriada, mensura a força da autocorrelação entre os valores de f{displaystyle mathrm {f} } separados por um atraso no tempo. Essa é uma maneira de procurar pela autocorrelação de f{displaystyle mathrm {f} } com o seu próprio passado. Ísso é útil para outras tarefas estatísticas além da análise dos sinais. Por exemplo, se f(t){displaystyle mathrm {f(t)} } representa a temperatura em um tempo t{displaystyle mathrm {t} }, espera-se uma forte correlação com a temperatura com um atraso temporal de 24 horas.

Ela possui uma transformada de Fourier,

Pf(ω)=∫−∞∞Rf(τ) e−iωτ dτ .{displaystyle mathrm {P_{f}(omega )=int _{-infty }^{infty }R_{f}(tau ) e^{-iomega tau } dtau .} }

Esta transformada de Fourier é chamada de função de densidade de potência espectral de f{displaystyle mathrm {f} }. (A não ser que todas componentes periódicas sejam primeiro filtradas de f{displaystyle mathrm {f} }, essa integral divergirá, porém é uma tarefa simples filtrar tais periodicidades.)

A potência espectral, como indicada por essa função de densidade P{displaystyle mathrm {P} }, mede a quantidade de variância contribuída às informações pela frequência ω{displaystyle omega }. Em sinais elétricos, a variância é proporcional à potência media(energia por unidade de tempo), e portanto a potêncial espectral descreve o quanto a diferença de frequências contribuem para a potência média do sinal. Este processo é chamado de análise espectral temporal e é análogo à usual análise de variância de informações que não são séries temporais.

Conhecimento de quais frequências são mais "importantes" nesse sentido é crucial para o design apropriado de filtros e para a escolha apropriada de aparatos medidores. Também pode ser útil para a análise científica de fenômenos responsáveis por produzir as informações.

A potência espectral de um sinal pode também ser aproximadamente medido diretamente mensurando a potência média que resta em um sinal depois que frequências externas sejam filtradas e removidas.

Análise espectral também é uma ferramenta de sinais visuais. A potência espectral ignora todas relações de fase, o que é considerado bom para muitos propósitos, mas para sinais de vídeo outros tipos de análise espectral devem ser empregados, ainda utilizando a transformada de Fourier como ferramenta principal.

Domínio complexo |

Transformada de Laplace |

A transformada de Fourier f^(ω){displaystyle mathrm {{hat {f}}(omega )} } é relacionada à transformada de Laplace F(s){displaystyle mathrm {F(s)} }, a qual também é utilizada para a solução de equações diferenciais e análise de filtros. É provável que uma função f{displaystyle mathrm {f} } para a qual a integral de Fourier não convirja no eixo R{displaystyle mathbb {R} } tenha uma transformada de Fourier complexa definida em alguma região do plano C{displaystyle mathbb {C} }.

Por exemplo, se f(t){displaystyle mathrm {f(t)} } é de crescimento exponencial, |f(t)|<C ea|t|{displaystyle mathrm {|f(t)|<C e^{a|t|}} }, para constantes C{displaystyle mathrm {C} } e a>0{displaystyle mathrm {a>0} }, então

f^(iτ)=∫−∞∞e2πτt f(t) dt ,{displaystyle mathrm {{hat {f}}(itau )=int _{-infty }^{infty }e^{2pi tau t} f(t) dt ,} }

convergente para todo 2πτ<−a{displaystyle mathrm {2pi tau <-a} }, é a transformada de Laplace bilateral.

A versão mais usual("unilateral") da transformada de Laplace é

F(s)=∫0∞f(t) e−st dt .{displaystyle mathrm {F(s)=int _{0}^{infty }f(t) e^{-st} dt .} }

Se f(t){displaystyle mathrm {f(t)} } também é causal, então

f^(iτ)=F(−2πτ) .{displaystyle mathrm {{hat {f}}(itau )=F(-2pi tau ) .} }

Além disso, ampliando a transformada de Fourier para o domínio complexo significa incluir a transformada de Laplace como um caso especial−{displaystyle mathrm {-} }o caso de funções causais−{displaystyle mathrm {-} }mas com a mudança de variável s=iω .{displaystyle mathrm {s=iomega .} }

Inversão |

Se f^{displaystyle mathrm {hat {f}} } não possui polos para a⩽τ⩽b{displaystyle mathrm {aleqslant tau leqslant b} }, então

∫−∞∞f^(σ+ia)eiωtdσ=∫−∞∞f^(σ+ib)eiωtdσ{displaystyle mathrm {int _{-infty }^{infty }{hat {f}}(sigma +ia)e^{iomega t}dsigma =int _{-infty }^{infty }{hat {f}}(sigma +ib)e^{iomega t}dsigma } }

pelo teorema da integral de Cauchy. Portanto, a fórmula da inversão de Fourier pode utilizar integração sobre diferentes linhas, paralelas ao eixo R{displaystyle mathbb {R} }.

Teorema: se f(t)=0{displaystyle mathrm {f(t)=0} } para t<0{displaystyle mathrm {t<0} } e |f(t)|<C ea|t|{displaystyle mathrm {|f(t)|<C e^{a|t|}} } para algumas constantes C{displaystyle mathrm {C} } e a>0 ,{displaystyle mathrm {a>0 ,} } então

f(t)=∫−∞∞f^(σ+iτ)eiωtdσ ,{displaystyle mathrm {f(t)=int _{-infty }^{infty }{hat {f}}(sigma +itau )e^{iomega t}dsigma ,} } para qualquer t<−a2π .{displaystyle mathrm {t<-{frac {a}{2pi }} .} }

Esse teorema implica na fórmula de inversão de Mellin para a transformação de Laplace,

f(t)=12πi∫b−i∞b+i∞F(s) est ds ,{displaystyle mathrm {f(t)={frac {1}{2pi i}}int _{b-iinfty }^{b+iinfty }F(s) e^{st} ds ,} }

para qualquer b>a ,{displaystyle mathrm {b>a ,} } onde F(s){displaystyle mathrm {F(s)} } é a transformada de Laplace de f(t) .{displaystyle mathrm {f(t) .} }

Métodos computacionais |

O método computacional apropriado depende principalmente de como a função matemática original é representada e da forma desejada de saída("output").

Como a definição fundamental de uma transformada de Fourier é uma integral, funções que podem ser expressadas como expressões de forma fechada("closed-form") são usualmente computadas trabalhando a integral analiticamente para obter uma expressão de forma fechada na variável conjugada como resultado. Este método é utilizado para gerar tabelas de transformadas de Fourier, incluindo aquelas encontradas nas tabelas abaixo.

Muitos sistemas computacionais algébricos como Matlab e Mathematica que são capazes de integração simbólica são capazes de computar as transformadas de Fourier analiticamente. Por exemplo, para computar a transformada de Fourier de f(t)=e−πt2cos(6πt){displaystyle mathrm {f(t)=e^{-pi t^{2}}cos(6pi t)} }, escreve-se int cos(6*pi*t) exp(-pi*t^2) exp(-i*2*pi*f*t) from -inf to inf em Wolfram Alpha.

Integração numérica de funções de forma fechada |

Se a função de entrada está em forma fechada e a função de saída desejada é uma série de pares ordenados sobre um domínio específico, então a transformada de Fourier pode ser gerada através de integração numérica em cada valor da variável conjugada de Fourier(frequência, por exemplo) para qual o valor da variável de saída é desejado. Nota-se que este método requere computar uma integração numérica separada para cada valor de frequência para qual o valor da transformada de Fourier é desejada. O método de integração numérica funciona em uma gama mais ampla de funções que o método analítico, porque produz resultados para funções que não possuem integrais de Fourier de forma fechada.

Integração numérica de uma série de pares ordenados |

Se a função de entrada é uma série de pares ordenados(por exemplo, uma série temporal a partir da mensuração de uma variável de saída repetidamente em um intervalo de tempo) então a função de saída deve ser uma série de pares ordenados(por exemplo, um número complexo vs. frequência sobre um domínio especificado de frequências), a não ser que que certas hipóteses e aproximações sejam adotadas, permitindo que a função de saída seja aproximada por uma expressão de forma fechada. No caso geral onde as séries de pares ordenados de entrada são consideradas serem amostras que representam uma função contínua sobre um intervalo (amplitude vs. tempo, por exemplo), a série de pares ordenados que representam a função de saída podem ser obtidos através de integração numérica da informação de entrada sobre o intervalo disponível em cada valor da variável conjugada de Fourier(frequência, por exemplo) para qual o valor da transformada de Fourier é desejada.

Integração numérica explícita sobre os pares ordenados pode trazer o valor de saída da transformada de Fourier para qualquer valor desejado da variável conjugada(frequência, por exemplo), para que um espectro possa ser produzido em qualquer tamanho de passo desejado e em qualquer raio de variável desejável para determinação precisa de amplitudes, frequências e fases. Diferentemente das limitações nos métodos DFT e FFT, integração numérica explícita pode ter qualquer tamanho de passo desejado e computar a transformada de Fourier sobre qualquer raio desejado da variável conjugada(por exemplo, frequência).

Fórmula de somatório de Poisson (PSF) |

A fórmula de somatório de Poisson (PSF) é uma equação que relaciona os coeficientes da série de Fourier de uma função com valores da Transformada de Fourier (que é contínua) da mesma função.

Consequentemente, o somatório periódico de uma função é definido completamente por trechos discretos da Transformada de Fourier da função original. Inversamente, o somatório periódico da Transformada de Fourier de uma função é completamente definido por trechos discretos da função original.

O somatório de Poisson relata que, para funções suficientemente regulares f{displaystyle f},

∑nf^(n)=∑nf(n){displaystyle sum _{n}{hat {f}}(n)=sum _{n}f(n)}.

Essa expressão possui uma variedade de formas úteis encontradas na literatura, que são obtidas pela aplicação das propriedades de Mudança de Escala e Deslocamento Temporal (no eixo t{displaystyle t}). A fórmula possui aplicações em áreas como engenharia, física e teoria dos números. A representação no domínio da frequência da fórmula de somatório de Poisson é também chamada de Transformada de Fourier de tempo discreto.

A fórmula de somatório de Poisson é geralmente associada com a física em meios condicionados em regime periódico, como no caso do problema da condução de calor em um círculo. A solução fundamental da equação do calor em um círculo é chamada de função teta. Ela é usada na teoria dos números para provar as propriedades de transformação das funções teta, que são um tipo de forma modular, e é mais usualmente relacionada à teoria de formas automórficas, onde ela aparece em um dos lados da fórmula do traço de Selberg.

Transformada discreta de Fourier |

(ver artigo principal Transformada Discreta de Fourier)

Para uso em computadores, seja para aplicações científicas ou em processamento digital de sinais, é preciso ter valores xk{displaystyle x_{k}} discretos. Para isso existe a versão da transformada para funções discretas.

xk=∑j=0n−1fje2πinjkk=0,…,n−1{displaystyle x_{k}=sum _{j=0}^{n-1}f_{j}e^{{frac {2pi i}{n}}jk}quad quad k=0,dots ,n-1}.

fj=1n∑k=0n−1xke−2πinjkj=0,…,n−1{displaystyle f_{j}={frac {1}{n}}sum _{k=0}^{n-1}x_{k}e^{-{frac {2pi i}{n}}jk}quad quad j=0,dots ,n-1}

Um método largamente utilizado para o cálculo computacional desta versão é a Transformada rápida de Fourier (em inglês fast Fourier transform, ou FFT), cuja complexidade é O(n log n) contra O(n²) necessários para o mesmo cálculo.

Algumas transformadas de Fourier^[15][16] |

Nesta tabela, δ(t){displaystyle delta (t),} é a delta de Dirac, u(t) é a função de passo Heaviside, sgn(t) é a função sinal, rect(t) é a função retangular, sinc(t) é a função sinc = sin⁡πtπt{displaystyle {frac {sin pi t}{pi t}}} e tri(t) é a função triangular.

Tabela 1 - Alguns pares de transformadas de Fourier
f(t){displaystyle f(t)}	F(ω){displaystyle F(omega )}
δ(t){displaystyle delta (t),!}	1{displaystyle 1,!}
δ(t−a){displaystyle delta (t-a),!}	e−iaω{displaystyle e^{-iaomega },!}
u(t){displaystyle u(t),!}	πδ(ω)+1iω{displaystyle pi delta (omega )+{frac {1}{iomega }},!}
1{displaystyle 1,!}	2πδ(ω){displaystyle 2pi delta (omega ),!}
sgn⁡(t){displaystyle operatorname {sgn} (t),!}	2iω{displaystyle {frac {2}{iomega }},!}
eiω0t{displaystyle e^{iomega _{0}t},!}	2πδ(ω−ω0){displaystyle 2pi delta (omega -omega _{0}),!}
cos⁡ω0t{displaystyle cos omega _{0}t,!}	π(δ(ω−ω0)+δ(ω+ω0)){displaystyle pi (delta (omega -omega _{0})+delta (omega +omega _{0})),!}
sin⁡ω0t{displaystyle sin omega _{0}t,!}	πi(δ(ω−ω0)−δ(ω+ω0)){displaystyle {frac {pi }{i}}(delta (omega -omega _{0})-delta (omega +omega _{0})),!}
rect⁡(ta){displaystyle operatorname {rect} left({frac {t}{a}}right),!}	|a|⋅sinc⁡(aω2π)=2ωsin⁡(ωa){displaystyle |a|cdot operatorname {sinc} left(a{frac {omega }{2pi }}right);=;{frac {2}{omega }}operatorname {sin} left({frac {omega }{a}}right),!}
cos⁡(ω0t)u(t){displaystyle cos(omega _{0}t)u(t),!}	π2(δ(ω−ω0)+δ(ω+ω0))+iωω02−ω2{displaystyle {frac {pi }{2}}(delta (omega -omega _{0})+delta (omega +omega _{0}))+{frac {iomega }{omega _{0}^{2}-omega ^{2}}},!}
sin⁡(ω0t)u(t){displaystyle sin(omega _{0}t)u(t),!}	π2i(δ(ω−ω0)−δ(ω+ω0))+ω2ω02−ω2{displaystyle {frac {pi }{2i}}(delta (omega -omega _{0})-delta (omega +omega _{0}))+{frac {omega ^{2}}{omega _{0}^{2}-omega ^{2}}},!}
rect⁡(t/a)cos⁡(ω0t){displaystyle operatorname {rect} (t/a)cos(omega _{0}t),!}	a(sinc⁡(ω−ω0)a2π+sinc⁡(ω+ω0)a2π){displaystyle aleft(operatorname {sinc} {frac {(omega -omega _{0})a}{2pi }}+operatorname {sinc} {frac {(omega +omega _{0})a}{2pi }}right),!}
sinc⁡(ta){displaystyle operatorname {sinc} left({frac {t}{a}}right),!}	|a|⋅rect⁡(ω2πa){displaystyle |a|cdot operatorname {rect} left({frac {omega }{2pi a}}right),!}
sinc2⁡(ta){displaystyle operatorname {sinc} ^{2}left({frac {t}{a}}right),!}	|a|⋅tri⁡(ω2πa){displaystyle |a|cdot operatorname {tri} left({frac {omega }{2pi a}}right),!}
e−atu(t),Re⁡(a)>0{displaystyle e^{-at}u(t),operatorname {Re} (a)>0,!}	1a+iω{displaystyle {frac {1}{a+iomega }},!}
tn{displaystyle t^{n},!}	2πinδn(ω){displaystyle 2pi i^{n}delta ^{n}(omega ),!}
tn−1e−atu(t),Re⁡(a)>0{displaystyle t^{n-1}e^{-at}u(t),operatorname {Re} (a)>0,!}	(n−1)!(a+iω)n{displaystyle {frac {(n-1)!}{(a+iomega )^{n}}},!}
e−a|t|,Re⁡(a)>0{displaystyle e^{-a|t|},operatorname {Re} (a)>0,!}	2aa2+ω2{displaystyle {frac {2a}{a^{2}+omega ^{2}}},!}
e−πt2{displaystyle e^{-pi t^{2}},!}	e−ω24π{displaystyle e^{-{frac {omega ^{2}}{4pi }}},!}
1|t|{displaystyle {frac {1}{sqrt {|t|}}},!}	2π|ω|{displaystyle {sqrt {frac {2pi }{|omega |}}},!}
1t2+a2{displaystyle {frac {1}{t^{2}+a^{2}}},!}	πae−a|ω|{displaystyle {frac {pi }{a}}e^{-a|omega |},!}
tri⁡(t){displaystyle operatorname {tri} (t),!}	sinc2⁡(ω2π){displaystyle operatorname {sinc} ^{2}left({frac {omega }{2pi }}right),!}

Transformada de Fourier de Funções Especiais^[17] |

Uma condição suficiente para que uma função possua uma transformada de Fourier é a seguinte:

∫−∞∞|f(t)|dt<∞{displaystyle int _{-infty }^{infty }|f(t)|dt<infty }

Geometricamente a condição impõe que a área abaixo da curva de |f(t)|{displaystyle |f(t)|} deve ser finita.

Essa condição não é uma restrição e sim uma garantia de que, caso satisfeita, há uma transformada de Fourier correspondente para tal função. No entanto, existem muitas outras funções que, apesar de não satisfazerem tal condição, também possuem transformada de Fourier. Algumas funções que pertencem a essa categoria especial são apresentadas a seguir.

Transformada de Fourier da Função Delta de Dirac |

A transformada da função delta de Dirac é dada por:

F{δ(t−a)}=∫−∞∞δ(t−a)e−iωtdt{displaystyle {mathcal {F}}{delta (t-a)}=int _{-infty }^{infty }delta (t-a)e^{-iomega t}dt}.

Pela propriedade da filtragem:

∫−∞∞δ(t−a)e−iωtdt=e−iωa{displaystyle int _{-infty }^{infty }delta (t-a)e^{-iomega t}dt=e^{-iomega a}}.

Logo a transformada da função delta de Dirac é dada por:

F{δ(t−a)}=e−iωa{displaystyle {mathcal {F}}{delta (t-a)}=e^{-iomega a}}

No caso especial em que a = 0 temos:

F{δ(t)}=∫−∞∞δ(t)e−iωtdt=e−iω0{displaystyle {mathcal {F}}{delta (t)}=int _{-infty }^{infty }delta (t)e^{-iomega t}dt=e^{-iomega 0}}.

Logo:

F{δ(t)}=1{displaystyle {mathcal {F}}{delta (t)}=1}

Transformada de Fourier de uma Função Periódica |

Uma função periódica pode ser representada em série de Fourier complexa da seguinte forma:

f(t)=∑n=−∞∞Cneiωnt{displaystyle f(t)=sum _{n=-infty }^{infty }C_{n}e^{iomega _{n}t}} onde Cn=1T∫−T2T2f(t)e−iωntdt{displaystyle C_{n}={frac {1}{T}}int _{-{frac {T}{2}}}^{frac {T}{2}}f(t)e^{-iomega _{n}t}dt}
e ωn=2πnT{displaystyle omega _{n}={frac {2pi n}{T}}}

Aplicando a transformada de Fourier na igualdade obtemos:

F{f(t)}=F{∑n=−∞∞Cneiωnt}{displaystyle {mathcal {F}}{f(t)}={mathcal {F}}left{sum _{n=-infty }^{infty }C_{n}e^{iomega _{n}t}right}}

A transformada de Fourier dada por F{f(t)}=∫−∞∞f(t)e−iωtdt{displaystyle {mathcal {F}}{f(t)}=int _{-infty }^{infty }f(t)e^{-iomega t}dt} é uma integral com respeito a uma variável, t nesse caso, e sendo a integral uma operação linear podemos tomar a transformada somente em relação aos termos que envolvem t:

F{f(t)}=∑n=−∞∞CnF{eiωnt}{displaystyle {mathcal {F}}{f(t)}=sum _{n=-infty }^{infty }C_{n}{mathcal {F}}left{e^{iomega _{n}t}right}}

Para calcular F{eiωnt}{displaystyle {mathcal {F}}left{e^{iomega _{n}t}right}} partimos da expressão deduzida na seção referente a transformada da função delta de Dirac:

F{δ(t)}=1{displaystyle {mathcal {F}}{delta (t)}=1}

Aplicamos a transformada inversa:

F−1{F{δ(t)}}=F−1{1}{displaystyle {mathcal {F}}^{-1}{{mathcal {F}}{delta (t)}}={mathcal {F}}^{-1}{1}}

δ(t)=12π∫−∞∞1eiωtdt{displaystyle delta (t)={frac {1}{2pi }}int _{-infty }^{infty }1e^{iomega t}dt}

Trocando t por -t:

δ(−t)=12π∫−∞∞1e−iωtdt{displaystyle delta (-t)={frac {1}{2pi }}int _{-infty }^{infty }1e^{-iomega t}dt}

(Observe que a troca de dt{displaystyle dt} por d(−t){displaystyle d(-t)} é neutralizada pela inversão dos limites de integração de −∞{displaystyle -infty } pra +∞{displaystyle +infty } e vice-versa)

Agora, permutando t e w:

2πδ(−w)=∫−∞∞1e−iωtdw{displaystyle 2pi delta (-w)=int _{-infty }^{infty }1e^{-iomega t}dw}

Fica evidente que:

2πδ(−w)=F{1}{displaystyle 2pi delta (-w)={mathcal {F}}{1}}

Devido a paridade da função delta de Dirac:

2πδ(−ω)=2πδ(ω){displaystyle 2pi delta (-omega )=2pi delta (omega )}

Temos que:

F{1}=2πδ(ω){displaystyle {mathcal {F}}{1}=2pi delta (omega )}

No entanto, pela propriedade do deslocamento no eixo de frequência, temos:

F{1eiωnt}=F{eiωnt}=2πδ(ω−ωn){displaystyle {mathcal {F}}{1e^{iomega _{n}t}}={mathcal {F}}{e^{iomega _{n}t}}=2pi delta (omega -omega _{n})}

Finalmente, a transformada de Fourier de uma função periódica é dada por:

F{f(t)}=2π∑n=−∞∞Cnδ(ω−ωn){displaystyle {mathcal {F}}{f(t)}=2pi sum _{n=-infty }^{infty }C_{n}delta (omega -omega _{n})}

O resultado demonstra que transformada de Fourier de qualquer função periódica é uma sequência de impulsos equidistantes.

Aplicação da Transformada de Fourier em problemas |

Utilização da transformada de Fourier para determinar a resposta em regime transitório de circuitos elétricos |

Utilizaremos a transformada de Fourier para determinar i_o(t) no circuito abaixo, sabendo que i_g(t) vale 20 sgn(t) amperes.

Primeiramente, calcula-se a transformada de Fourier da fonte de corrente:

Ig(w)=F{20sgn(t)}{displaystyle Ig(w)={mathcal {F}}left{20sgn(t)right}}

=20(2jw){displaystyle =20{biggl (}{frac {2}{jw}}{biggr )}}

=40jw{displaystyle ={frac {40}{jw}}}

A função de transferência do circuito é a razão entre I_o e I_g, desta maneira:

H(w)=IoIg=14+jw{displaystyle H(w)={frac {Io}{Ig}}={frac {1}{4+jw}}}

A transformada de Fourier de io(t) é a seguinte:
H(ω) = I_g(ω)H(ω)

=40jw(4+jw){displaystyle ={frac {40}{jw(4+jw)}}}

Ao expandir I_o(ω) em uma soma de frações parciais, temos:

Io(w)=C1jw+C24+jw{displaystyle Io(w)={frac {C1}{jw}}+{frac {C2}{4+jw}}}

Analisando C1 e C2, obtemos:

C1=404=10,{displaystyle C1={frac {40}{4}}=10,}

C2=40−4=−10.{displaystyle C2={frac {40}{-4}}=-10.}

Portanto,

Io(w)=10jw−104+jw.{displaystyle Io(w)={frac {10}{jw}}-{frac {10}{4+jw}}.}

Logo, a resposta para Io(t) é:

io(t)=F−1{Io(w)}{displaystyle io(t)={mathcal {F}}^{-1}{Io(w)}}

=5sgn(t)−10e−4tu(t).{displaystyle =5sgn(t)-10e^{-4t}u(t).}

Vale observar que uma característica importante da transformada de Fourier é que ela fornece, de maneira direta, a resposta de regime permanente do circuito quando a entrada é do tipo senoidal.

Circuitos RLC em série |

A transformada de Fourier também pode ser utilizada para a resolução de funções ordinárias. Como exemplo podemos tratar de circuitos RLC em série com o objetivo de encontrar a função de transferência entre a tensão de saída e a tensão de entrada do circuito.

• 
  

  

  
  

  
  

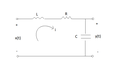
  Circuito RLC
  

  
  

  
  

Vamos considerar  como a função de transferência:

H(ω)=Y(ω)X(ω){displaystyle H(omega )={{Y(omega )} over {X(omega )}}}

Primeiramente podemos utilizar a Lei de Kirchhoff para obter o seguinte:

−x(t)+Vl+Vr+y(t)=0{displaystyle -x(t)+Vl+Vr+y(t)=0}

Na qual   Vl{displaystyle Vl}e Vr{displaystyle Vr}  correspondem às quedas de tensão no indutor e no resistor, respectivamente. Ou seja:

Vl=Ldidt{displaystyle Vl=L{di over dt}} e Vr=Ri{displaystyle Vr=Ri}

Substituindo na equação obtemos:

x(t)=Ldidt+Ri+y(t){displaystyle x(t)=L{di over dt}+Ri+y(t)}

A corrente pode, ainda, ser descrita em função de y ou de x, considerando a corrente que passa no circuito como a própria corrente que passa no capacitor. Para isso utilizamos a seguinte relação:

ic=i=Cddty(t){displaystyle ic=i=C{d over dt}y(t)}

Substituindo na equação podemos obter:

x(t)=LCd2dt2y(t)+RCddty(t)+y(t){displaystyle x(t)=LC{operatorname {d} !^{2} over operatorname {d} !t^{2}}y(t)+RC{d over dt}y(t)+y(t)}

Fazendo a transformada de Fourier nos dois lados da igualdade e aplicando o método da linearidade obtemos:

F{x(t)}=F{LCd2dt2y(t)}+F{RCddty(t)}+F{y(t)}{displaystyle {mathcal {F}}{x(t)}={mathcal {F}}{LC{d^{2} over dt^{2}}y(t)}+{mathcal {F}}{RC{d over dt}y(t)}+{mathcal {F}}{y(t)}}

Utilizando o método da transformada da derivada segunda em F{LCd2dt2y(t)}{displaystyle {mathcal {F}}{LC{d^{2} over dt^{2}}y(t)}}, da transformada da derivada primeira em F{RCddty(t)}{displaystyle {mathcal {F}}{RC{d over dt}y(t)}} e colocando Y(ω){displaystyle Y({mathcal {omega }})}  em evidência chegamos na equação abaixo:

X(ω)=Y(ω)(−ω2LC+jωRC+1){displaystyle X(omega )=Y(omega )(-omega ^{2}LC+jomega RC+1)}

Isolando Y(ω)X(ω){displaystyle {Y(omega )} over {X(omega })}e substituindo-o pela função de transferência H(ω){displaystyle H({mathcal {omega }})}  temos a equação:

Y(ω)X(ω=H(ω)=1(−ω2LC+jωRC+1){displaystyle {{Y(omega )} over {X(omega }}=H({mathcal {omega }})={1 over (-{mathcal {omega }}^{2}LC+j{mathcal {omega }}RC+1)}}

Deixando em função do tempo temos:

y(t)=F−1{H(ω)}∗x(t){displaystyle y(t)={mathcal {F}}^{-1}{{H({mathcal {omega }})}}*x(t)}

Equação do Calor |

Considere o problema evolutivo de difusão de temperatura numa barra infinita, dado pela equação de calor

∂u∂t(x,t)=μ∂2u∂t2(x,t), x ϵ (−∞,∞),t>0{displaystyle {partial u over partial t}(x,t)=mu {partial ^{2}u over partial t^{2}}(x,t), x epsilon (-infty ,infty ),t>0}

u(x,0)=f(x){displaystyle u(x,0)=f(x)}

Tomando a transformada de Fourier desse problema na variável x, obtemos

∂(Fx [u(x,t)])∂t=−μk2(Fx [u(x,t)]){displaystyle {partial (F_{x} [u(x,t)]) over partial t}=-mu k^{2}(F_{x} [u(x,t)])}

Fx [u(x,0)]=Fx [f(x)]{displaystyle F_{x} [u(x,0)]=F_{x} [f(x)]}

onde se usou a propriedade 2 da transformada da derivada.

Denotando Fx [u(x,t)]:=U(k,t){displaystyle F_{x} [u(x,t)]:=U(k,t)}, podemos escrever o problema de uma forma mais limpa:

∂U∂t=−μk2U{displaystyle {partial U over partial t}=-mu k^{2}U}

U(k,0)=F(k){displaystyle U(k,0)=F(k)}

Essa é uma equação que pode ser resolvida por várias métodos, entre eles separação de variáveis:

1U∂U∂t=−μk2{displaystyle {1 over U}{partial U over partial t}=-mu k^{2}}

ln(U)=−μk2t+C{displaystyle ln(U)=-mu k^{2}t+C}

U=e−μk2t+C=Ke−μk2t{displaystyle U=e^{-mu k^{2}t+C}=Ke^{-mu k^{2}t}}

onde K=eC{displaystyle K=e^{C}} é uma constante de integração que é calculada om a condição inicial:

U(k,0)=Ke−μk2.0=F(k)⇒K=F(k){displaystyle U(k,0)=Ke^{-mu k^{2}.0}=F(k)Rightarrow K=F(k)}

Logo,

U(k,t)=Fx(u(x,t))=F(k)e−μk2t{displaystyle U(k,t)=F_{x}(u(x,t))=F(k)e^{-mu k^{2}t}}

Agora, precisamos calcular a transformada inversa de U(k,t){displaystyle U(k,t)} para obter a solução u(x,t){displaystyle u(x,t)} do problema original.

Temos que

Fk−1(e−k2)=12πe−x24{displaystyle F_{k}^{-1}(e^{-k^{2}})={1 over 2{sqrt {pi }}}e^{-x^{2} over 4}}

Usando a propriedade de mudança de escala com a=μt{displaystyle a={sqrt {mu t}}} temos

Fk−1(e−μtk2)=Fk−1(e−μtk2)=12π1μte(−xμt)24{displaystyle F_{k}^{-1}(e^{-mu tk^{2}})=F_{k}^{-1}(e^{-{sqrt {mu tk}}^{2}})={1 over 2{sqrt {pi }}}{1 over {sqrt {mu t}}}e^{(-{x over {sqrt {mu t}}})^{2} over 4}}

ou seja,

Fk−1(e−μtk2)=14πμte−x24μt{displaystyle F_{k}^{-1}(e^{-{sqrt {mu tk}}^{2}})={1 over {sqrt {4pi mu t}}}e^{-{x^{2} over 4mu t}}}

Aplicando esse resultado juntamente com o teorema da convolução na equação, obtemos

u(x,t)=14πμt∫−∞∞f(y)e−(x−y)24μtdy{displaystyle u(x,t)={1 over {sqrt {4pi mu t}}}int _{-infty }^{infty }f(y)e^{-{(x-y)^{2} over 4mu t}}dy}

Equação do calor com termo fonte |

A difusão de temperatura numa barra infinita com um termo fonte é dada por:

∂u∂t=μ∂2u∂t2+f(x,t), x ϵ (−∞,∞),t>0{displaystyle {partial u over partial t}=mu {partial ^{2}u over partial t^{2}}+f(x,t), x epsilon (-infty ,infty ),t>0}

u(x,0)=0{displaystyle u(x,0)=0}

Fazendo a transformada de Fourier em x temos:

∂(Fx [u(x,t)])∂t=−μk2(Fx [u(x,t)])+Fx[f(x,t)]{displaystyle {partial (F_{x} [u(x,t)]) over partial t}=-mu k^{2}(F_{x} [u(x,t)])+F_{x}[f(x,t)]}

Fx[u(x,0)]=0{displaystyle F_{x}[u(x,0)]=0}

Denotando Fx [u(x,t)]:=U(k,t){displaystyle F_{x} [u(x,t)]:=U(k,t)}, temos:

∂U∂t=−μk2U+F{displaystyle {partial U over partial t}=-mu k^{2}U+F}

U(k,0)=0{displaystyle U(k,0)=0}

Esta equação diferencial é resolvida por fator integrante:

∂U∂t+μk2U=F{displaystyle {partial U over partial t}+mu k^{2}U=F}

eμk2t∂U∂t+eμk2tμk2U=eμk2tF{displaystyle e^{mu k^{2}t}{partial U over partial t}+e^{mu k^{2}t}mu k^{2}U=e^{mu k^{2}t}F}

∂∂t(Ueμk2t)=eμk2tF{displaystyle {partial over partial t}(Ue^{mu k^{2}t})=e^{mu k^{2}t}F}

U(k,t)eμk2t−U(k,0)eμk20=∫0teμk2τF(k,τ)dτ{displaystyle U(k,t)e^{mu k^{2}t}-U(k,0)e^{mu k^{2}0}=textstyle int limits _{0}^{t}displaystyle e^{mu k^{2}tau }F(k,tau )dtau }

U(k,t)=e−μk2t∫0teμk2τF(k,τ)dτ{displaystyle U(k,t)=e^{-mu k^{2}t}textstyle int _{0}^{t}displaystyle e^{mu k^{2}tau }F(k,tau )dtau }

U(k,t)=Fx[u(x,t)]=∫0te−μ(t−τ)k2F(k,τ)dτ{displaystyle U(k,t)=F_{x}[u(x,t)]=textstyle int _{0}^{t}displaystyle e^{-mu (t-tau )k^{2}}F(k,tau )dtau }

Fazendo a transformada inversa, temos:

Fx−1[e−μ(t−τ)k2]=14πμ(t−τ)e−x24μ(t−τ){displaystyle F_{x}^{-1}[e^{-mu (t-tau )k^{2}}]={frac {1}{sqrt {4pi mu (t-tau )}}}e^{-{frac {x^{2}}{4mu (t-tau )}}}}

Pelo teorema da convolução, temos:

u(x,t)=∫0t(Fx−1[e−μ(t−τ)k2]∗f(x,τ))dτ{displaystyle u(x,t)=textstyle int limits _{0}^{t}displaystyle (F_{x}^{-1}[e^{-mu (t-tau )k^{2}}]*f(x,tau ))dtau }

u(x,t)=∫0t[(14πμ(t−τ)e−x24μ(t−τ))∗f(x,τ)]dτ{displaystyle u(x,t)=textstyle int limits _{0}^{t}displaystyle [({frac {1}{sqrt {4pi mu (t-tau )}}}e^{-{frac {x^{2}}{4mu (t-tau )}}})*f(x,tau )]dtau }

u(x,t)=14πμ∫0t[1(t−τ)∫−∞∞e−(x−y)24μ(t−τ)f(y,τ)dy]dτ{displaystyle u(x,t)={frac {1}{sqrt {4pi mu }}}textstyle int limits _{0}^{t}displaystyle [{frac {1}{sqrt {(t-tau )}}}textstyle int limits _{-infty }^{infty }displaystyle e^{-{frac {(x-y)^{2}}{4mu (t-tau )}}}f(y,tau )dy]dtau }

Utilização da transformada de Fourier para obter a equação da difusão do sal em uma tubulação longa |

Considere o fenômeno de difusão de sal ao longo de um cano longo e fino. Supondo que uma quantidade Q{displaystyle Q} de sal foi introduzida no ponto x0{displaystyle x_{0}}, temos as seguintes equações:

Tubulação com uma certa quantidade de sal introduzida no ponto x0.

∂ρ∂t=μ∂2ρ∂x2{displaystyle {partial rho over partial t}=mu {partial ^{2}rho over partial x^{2}}} , com −∞<x<∞{displaystyle -infty <x<infty } e t>0{displaystyle t>0}

ρ(x,o)=QAδ(x−x0){displaystyle rho (x,o)={Q over A}delta (x-x_{0})}

Onde:

ρ=ρ(x,t)→{displaystyle rho =rho (x,t)rightarrow } concentração de sal

x→{displaystyle xrightarrow } variável espacial

t→{displaystyle trightarrow } variável temporal

μ→{displaystyle mu rightarrow } Coeficente de Difusão

Q→{displaystyle Qrightarrow } quantidade de sal

A→{displaystyle Arightarrow } área da seção transversal

Solução: Aplica-se a transformada de Fourier:

{Fx{∂ρ∂t}=μFx{∂2ρ∂x2}Fx{ρ(x,0)}=QAFx{δ(x−xo)}{displaystyle {begin{cases}F_{x}{begin{Bmatrix}{partial rho over partial t}end{Bmatrix}}=mu F_{x}{begin{Bmatrix}{partial ^{2}rho over partial x^{2}}end{Bmatrix}}\F_{x}{begin{Bmatrix}rho (x,0)end{Bmatrix}}={Q over A}F_{x}{begin{Bmatrix}delta (x-x_{o})end{Bmatrix}}end{cases}}}

e temos:

∂Fx{ρ}=−μk2Fx{ρ}{displaystyle partial F_{x}{rho }=-mu k^{2}F_{x}{rho }}

Fx{ρ(x,0)}=QAe−ix0k{displaystyle F_{x}{rho (x,0)}={Q over A}e^{-ix_{0}k}}, onde usou-se as propriedades da linearidade, transformada da derivada (com i2=−1{displaystyle i^{2}=-1}) e a propriedade da filtragem de Fourier.

Para facilitar o cálculo colocaremos Fx{ρ}=Γ{displaystyle F_{x}{rho }=Gamma } e teremos:

{∂Γ∂t=−μk2ΓΓ(k,0)=QAe−ix0k{displaystyle {begin{cases}{partial Gamma over partial t}=-mu k^{2}Gamma \Gamma (k,0)={Q over A}e^{-ix_{0}k}end{cases}}}

Resolvemos a primeira equação (Equação diferencial ordinária) no tempo t:

∂ΓΓ=−μk2∂t{displaystyle {partial Gamma over Gamma }=-mu k^{2}partial t}

e temos:

⟶ln|Γ|=−μk2t+C{displaystyle longrightarrow ln|Gamma |=-mu k^{2}t+C}

⟶Γ=e−μk2teC=μe−μk2t{displaystyle longrightarrow Gamma =e^{-mu k^{2}t}e^{C}=mu e^{-mu k^{2}t}}, onde μ=eC{displaystyle mu =e^{C}}

Como Γ(k,0)=QAe−ix0k{displaystyle Gamma (k,0)={Q over A}e^{-ix_{0}k}} e Γ(k,0)=μe−uk2.0{displaystyle Gamma (k,0)=mu e^{-uk^{2}.0}},

μ=QAe−ix0k{displaystyle mu ={Q over A}e^{-ix_{0}k}}

⇒Γ(k,t)=QAe−ix0ke−μk2t{displaystyle Rightarrow Gamma (k,t)={Q over A}e^{-ix_{0}k}e^{-mu k^{2}t}}

Agora calculamos a solução aplicando a transformada inversa de Fourier:

Fx−1{QAe−ix0k}=QAδ(x−x0){displaystyle F_{x}^{-1}left{{Q over A}e^{-ix_{0}k}right}={Q over A}delta (x-x_{0})}

Fx−1{e−μk2t}=12π∫−∞∞e−μk2teikxdk{displaystyle F_{x}^{-1}{e^{-mu k^{2}t}}={1 over 2pi }int limits _{-infty }^{infty }e^{-mu k^{2}t}e^{ikx}dk} lembrando que a transformada de Fourier depende de x{displaystyle x} e k{displaystyle k} somente

=1π∫0∞e−μk2tcos(kx)dk{displaystyle ={1 over pi }int limits _{0}^{infty }e^{-mu k^{2}t}cos(kx)dk}

Obs.: para seguirmos para o próximo passo é interessante lembrar que ∫0∞e−a2x2cos(mx)dx=π2ae−m24a,a>0{displaystyle int limits _{0}^{infty }e^{-a^{2}x^{2}}cos(mx)dx={{sqrt {pi }} over 2a}e^{-m^{2} over 4a},a>0},{displaystyle ,} onde x→k,m→x,a2=ut/a=ut{displaystyle xrightarrow k,mrightarrow x,a^{2}=ut/a={sqrt {ut}}}

Assim temos: Fx−1{e−μk2t}=1ππ2ute−z24ut=14πute−x24ut{displaystyle F_{x}^{-1}{e^{-mu k^{2}t}}={1 over pi }{{sqrt {pi }} over 2{sqrt {ut}}}e^{-{z^{2} over 4ut}}={1 over {sqrt {4pi ut}}}e^{-{x^{2} over 4ut}}}

Portanto: ρ(x,t)=∫−∞∞QAδ(y−x0)14πute−(x−y)24utdy{displaystyle rho (x,t)=int limits _{-infty }^{infty }{Q over A}delta (y-x_{0}){1 over {sqrt {4pi ut}}}e^{-{(x-y)^{2} over 4ut}}dy}

ρ(x,t)=QA4πute−(x−x0)24ut{displaystyle rho (x,t)={Q over A{sqrt {4pi ut}}}e^{-(x-x_{0})^{2} over 4ut}}

Vibrações livres transversais |

Considere o problema de vibrações livres transversais de uma barra infinita governada por

∂4y∂x4+1a2∂2y∂t2=0{displaystyle {frac {partial ^{4}y}{partial x^{4}}}+{frac {1}{a^{2}}}{frac {partial ^{2}y}{partial t^{2}}}=0} t>0,x∈(−∞,∞){displaystyle t>0,xin (-infty ,infty )}

y(x,0)=f(x){displaystyle y(x,0)=f(x)}

∂y∂t(x,0)=ag″(x){displaystyle {frac {partial y}{partial t}}(x,0)=ag''(x)}

Aplicando a transformada de Fourier e tomando a notação Y(k,t)=F{y(x,t)}{displaystyle Y(k,t)={mathcal {F}}{y(x,t)}}, obtemos:

∂2Y∂t2+k4a2Y=0{displaystyle {frac {partial ^{2}Y}{partial t^{2}}}+k^{4}a^{2}Y=0}

Y(0)=F{f}=F(k){displaystyle Y(0)={mathcal {F}}{f}=F(k)}

∂Y∂t(0)=−ak2G(k){displaystyle {frac {partial Y}{partial t}}(0)=-ak^{2}G(k)}

tendo a solução

Y(k,t)=F(k)cos(ak2t)−G(k)sin(ak2t){displaystyle Y(k,t)=F(k)cos(ak^{2}t)-G(k)sin(ak^{2}t)}

Tomando a transformada inversa de Fourier, obtemos:

y(k,t)=12π∫−∞∞F(k)cos(ak2t)eikxdk−12π∫−∞∞G(k)sin(ak2t)eikxdk{displaystyle y(k,t)={frac {1}{2pi }}int limits _{-infty }^{infty }F(k)cos(ak^{2}t)e^{ikx}dk-{frac {1}{2pi }}int limits _{-infty }^{infty }G(k)sin(ak^{2}t)e^{ikx}dk}

Usando o fato que

∫−∞∞e−k2aeikxdk=πae−x24a{displaystyle int limits _{-infty }^{infty }e^{-k^{2}a}e^{ikx}dk={frac {sqrt {pi }}{sqrt {a}}}e^{-{frac {x^{2}}{4a}}}}

e

1(ai)12=1ae−i14π{displaystyle {frac {1}{(ai)^{frac {1}{2}}}}={frac {1}{sqrt {a}}}e^{-i{frac {1}{4}}pi }}

trocamos a{displaystyle a} por ai{displaystyle ai} para obter:

12π∫−∞∞(cos(ak2t)−isin(ak2t))eikxdk=12πaei(x24a−π4){displaystyle {frac {1}{2pi }}int limits _{-infty }^{infty }(cos(ak^{2}t)-isin(ak^{2}t))e^{ikx}dk={frac {1}{2{sqrt {pi a}}}}e^{i({frac {x^{2}}{4a}}-{frac {pi }{4}})}}

Tomando as partes real e imaginária nesta equação, obtemos que:

12π∫−∞∞cos(ak2t)eikxdk=24πa(cos(x24a)+sin(x24a)){displaystyle {frac {1}{2pi }}int limits _{-infty }^{infty }cos(ak^{2}t)e^{ikx}dk={frac {sqrt {2}}{4{sqrt {pi a}}}}{biggl (}cos{biggl (}{frac {x^{2}}{4a}}{biggl )}+sin{biggl (}{frac {x^{2}}{4a}}{biggl )}{biggl )}}

e

12π∫−∞∞sin(ak2t)eikxdk=24πa(cos(x24a)−sin(x24a)){displaystyle {frac {1}{2pi }}int limits _{-infty }^{infty }sin(ak^{2}t)e^{ikx}dk={frac {sqrt {2}}{4{sqrt {pi a}}}}{biggl (}cos{biggl (}{frac {x^{2}}{4a}}{biggl )}-sin{biggl (}{frac {x^{2}}{4a}}{biggl )}{biggl )}}

Utilizando o resultado sobre convoluções, obtemos que:

12π∫−∞∞F(k)cos(ak2t)e−ikxdk=24πat∫−∞∞f(x−y)[cos(y24at)+sin(y24at)]dy{displaystyle {frac {1}{2pi }}int limits _{-infty }^{infty }F(k)cos(ak^{2}t)e^{-ikx}dk={frac {sqrt {2}}{4{sqrt {pi at}}}}int limits _{-infty }^{infty }f(x-y){biggl [}cos{biggl (}{frac {y^{2}}{4at}}{biggl )}+sin{biggl (}{frac {y^{2}}{4at}}{biggl )}{biggl ]}dy}

e

12π∫−∞∞G(k)cos(ak2t)e−ikxdk=24πat∫−∞∞g(x−y)[cos(y24at)−sin(y24at)]dy{displaystyle {frac {1}{2pi }}int limits _{-infty }^{infty }G(k)cos(ak^{2}t)e^{-ikx}dk={frac {sqrt {2}}{4{sqrt {pi at}}}}int limits _{-infty }^{infty }g(x-y){biggl [}cos{biggl (}{frac {y^{2}}{4at}}{biggl )}-sin{biggl (}{frac {y^{2}}{4at}}{biggl )}{biggl ]}dy}

ou seja,

y(x,t)=122πat∫−∞∞f(x−y)[cos(y24at)+sin(y24at)]dy−122πat∫−∞∞g(x−y)[cos(y24at)−sin(y24at)]dy{displaystyle y(x,t)={frac {1}{2{sqrt {2pi at}}}}int limits _{-infty }^{infty }f(x-y){biggl [}cos{biggl (}{frac {y^{2}}{4at}}{biggl )}+sin{biggl (}{frac {y^{2}}{4at}}{biggl )}{biggl ]}dy-{frac {1}{2{sqrt {2pi at}}}}int limits _{-infty }^{infty }g(x-y){biggl [}cos{biggl (}{frac {y^{2}}{4at}}{biggl )}-sin{biggl (}{frac {y^{2}}{4at}}{biggl )}{biggl ]}dy}

Escrevendo u2=y24at{displaystyle u^{2}={frac {y^{2}}{4at}}}, obtemos:

y(x,t)=12π∫−∞∞f(x−2ua12t12)(cos(u2)+sin(u2))du−12π∫−∞∞g(x−2ua12t12)(sin(u2)−cos(u2))du{displaystyle y(x,t)={frac {1}{sqrt {2pi }}}int limits _{-infty }^{infty }f(x-2ua^{frac {1}{2}}t^{frac {1}{2}})(cos(u^{2})+sin(u^{2}))du-{frac {1}{sqrt {2pi }}}int limits _{-infty }^{infty }g(x-2ua^{frac {1}{2}}t^{frac {1}{2}})(sin(u^{2})-cos(u^{2}))du}^[14]

Curiosidades |

Aplicação na conversão de gravações |

Um arquivo de áudio, quando gravado em sua totalidade por uma gravadora, ocupa um grande espaço para seu armazenamento e, consequentemente, causa lentidão no aparelho em que será reproduzido. A conversão feita para arquivos do tipo MP3, por exemplo, que podem ser armazenados em pequenos espaços e reproduzidos muito mais rápido, necessitam da transformada de Fourier.

A gravação inicial de um áudio capta todas as frequências, mesmo as que quase não aparecem no som ou as que não são audíveis pelo ouvido humano. A gravação aparece como uma onda que varia com senos e cossenos e essa onda pode ser escrita como uma função em relação ao tempo.

Supondo que a equação da gravação, que é a amostragem da função seja dada por f1(t){displaystyle f_{1}(t)}, pode-se defini-la por: f1(t)=f(t)∑n=−∞∞δ(t−nT){displaystyle f_{1}(t)=f(t)textstyle sum _{n=-infty }^{infty }displaystyle delta (t-nT)} onde T{displaystyle T} é o período da função inicial. Aqui a primeira função foi reescrita como uma outra função multiplicando um Delta de Dirac em todo o espaço da função analisada.

Usando-se a propriedade da filtragem para o Delta, pode-se reescrever f1(t){displaystyle f_{1}(t)} como:

f1(t)=1T∑−∞∞f(t)eiwnt{displaystyle f1(t)={frac {1}{T}}sum _{-infty }^{infty }f(t)e^{iwnt}}.

Ao se aplicar a transformada de Fourier na função tem-se que:

F1(w)=1T∑−∞∞F{f(t)eiwnt}{displaystyle F1(w)={frac {1}{T}}sum _{-infty }^{infty }{mathcal {F}}{{f(t)e^{iwnt}}}} e usando a propriedade da translação:

F1(w)=1T∑−∞∞F(w−wn){displaystyle F1(w)={frac {1}{T}}sum _{-infty }^{infty }F(w-wn)}

Como a função inicial f1(t){displaystyle f1(t)} é a gravação, pode encontrar o valor de F1(w){displaystyle F1(w)} fazendo sua transformada e consequentemente pela equação acima pode-se encontrar o valor de F(w){displaystyle F(w)}. Com isso, tem-se que:

f(t)=12π∫−∞∞F(w)eiwtdw{displaystyle f(t)={frac {1}{2pi }}int limits _{-infty }^{infty }F(w)e^{iwt}dw}

Onde a função f(t){displaystyle f(t)} é a conversão para um arquivo muito mais leve e de fácil reprodução.

Em suma, nesse caso, a transformada consegue reconhecer as frequências que são dominantes na música e apresenta apenas as principais notas que compõe o harmônico daquele momento. Os limites da análise, que estão variando ao infinito, na transformada são reduzidos para os limites em que a frequência pode ser ouvida pelo ouvido humano, assim, o que resta são as principais frequências (harmônicos). A nova função tem vantagens pois será reproduzido apenas o que realmente é necessário no áudio.

Um outro exemplo é o Ogg Vorbis, formato de arquivo utilizado pelo Spotify em seu aplicativo de Desktop. O Vorbis usa uma versão computacional extremamente rápida da transformada de fourier, chamada de transformada discreta de cossenos. Outro aplicativo de áudio extremamente famoso: Shazam, utiliza da transformada, por meio de um banco de frequências distintas em canções que compara com que é colocado para o mesmo ouvir.

Fones de ouvido com cancelamento de ruído utilizam da Transformada de Fourier ,um microfone grava o ruído do ambiente ao redor, mede o conteúdo da freqüência em todo o espectro, e, em seguida, inverte o conteúdo para adicionar um som em seu mix de áudio que irá anular todos os sons indesejados ao seu redor.

^[18][19]

Processamento de Imagens |

Pode-se entender filtragem de uma imagem como suas respectivas técnicas de transformações aplicadas a cada pixel da imagem, levando em conta os níveis de cinza de uma região vizinha de cada pixel desta imagem. Tais técnicas se dividem basicamente em duas:

- Filtragem no Domínio Espacial

-Filtragem no Domíno Frequência

A filtragem no domínio frequência é baseada no teorema da convolução. Esse processamento de imagens no domínio da frequência é realizado basicamente em 3 passos:

1 - A imagem é transformada do Domínio Espacial para o Domínio Frequência, pela Transformada de Fourier.

2 - Operações são realizadas na imagem.

3 - Para que a imagem possa ser visível ao olho humano, então ocorre o processo inverso, onde a imagem no domínio frequência é transformada para o domínio espacial. Este último passo é feito pela Transformada Inversa de Fourier.

A transformada de Fourier possui algumas propriedades que facilitam a sua utilização em aplicações computacionais, tais como: separabilidade, translação, periodicidade e simetria conjugada, rotação, distributividade, mudança de escala, valor médio, laplaciano, convolução, correlação e amostragem. Dentre essas, a propriedade da Convolução é de fundamental importância para a compreensão das técnicas de processamento de imagens baseadas na transformada de Fourier.

De uma forma geral a convolução de uma imagem com outra imagem, forma uma terceira imagem. Essa convolução entre duas funções no domínio espacial tem como transformada a multiplicação das transformadas das duas funções no domínio frequência. Após discretização da imagem utilizando o algoritmo FFT(Fast Fourier Transform) a imagem está convoluída com o filtro, assim é aplicada a transformada inversa para retorno ao domínio espacial.

Uma informação importante que se pode obter pelo espectro de fourier é a informação da força da imagem (image power), que é uma informação bastante importante quando se é necessário determinar o filtro a ser aplicado a imagem, sendo possível determinar o quanto em percentagem a imagem será retida ou atenuada.

A filtragem mais simples utilizada é realizada através de um filtro passa faixa ou passa banda, removendo então regiões selecionadas de frequências entre altas e baixas frequências.

Notas |

Ver também |

• Transformada de Laplace


• Série de Fourier


• Análise harmónica


• Transformada discreta de cosseno


• Transformada de Hartley


• Transformada de Hilbert


• Processamento de Imagens

Ligações externas |

• 
  All of Mathcad (em inglês)


• 
  Determinação online da transformada ou da inversa da transformada, wims.unice.fr


• Biblioteca em Java


• 
  Equações Diferenciais e Equações de Diferenças,Jaime.E.Villate (em português)

Referências

21.REAMAT, Recursos Educacionais Abertos de Matemática. Universidade Federal do Rio Grande do Sul.